Teorema de Pick

El Teorema de Pick és un teorema que ens permet calcular l'àrea de polígons simples reticulars. El Teorema va ser formulat pel matemàtic Georg Pick l'any 1899, però no va ser del tot conegut fins a l'any 1969, quan va ser publicat en el llibre matemàtic Mathematical Snapshots.^[1]

Explicació del Teorema

La fórmula que ens dona el Teorema per calcular l'àrea és: ${\textstyle A=i+{\frac {b}{2}}-1}$.^[2] On A representa l'àrea del polígon en unitats quadrades, i representa els punts interiors del polígon i b representa els punts de la frontera del polígon. Per poder entendre el Teorema cal definir els conceptes de polígon simple reticular, punts, punts interiors i punts frontera.

Polígon reticular Simple

S'entén com a polígon simple un polígon tal que els seus costats no s'intersequen, és a dir, que no es tallen entre si. De manera que divideix el pla en dos regions, una exterior al polígon i una regió interna. I un polígon reticular és un polígon que podem situar tots els seus vèrtex en punts de coordenades enteres, és a dir, a sobre d'una quadrícula o retícula.^[3]

• 
  Aquest és un exemple d'un polígon simple reticular.
• 
  Aquest és un altre polígon simple reticular, amb un altre tipus d'angles.
• 
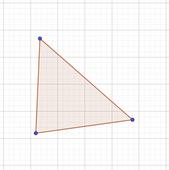  Aquest és un polígon simple, encara que no reticular
• 
  Aquest és un exemple de polígon reticular però no simple

Punts

Quan parlem de punts en aquest context ens referim a punts de coordenades enteres, és a dir, punts reticulars situats a sobre de la quadrícula.

Punts interiors

Els punts interiors seran els punts reticulars que es troben a la regió interna del polígon, sense comptar els punts situats a sobre dels seus costats.

Punts frontera

Els punts frontera són els punts reticulars que es troben a sobre dels costats del polígon.

Demostració del Teorema

Una de les particularitats d'aquest teorema és que es pot demostrar de diverses maneres. Com ara bé, la demostració amb la fórmula d'Euler, amb el Teorema de Minkowski, o amb la teoria de difusió del calor.^[1] Però nosaltres explicarem la més fàcil d'entendre, a més a més de ser la més intuïtiva, la demostració clàssica^[4].

Aquesta demostració clàssica consta de tres passos. Primerament demostra que tot polígon simple es pot triangular^[5], després demostra que el Teorema de Pick és vàlid per a qualsevol mena de triangle^[6], i per últim, demostra que podem aplicar la fórmula de Pick a dos polígons amb interiors diferents però amb un costat en comú i la suma dels resultats és l'àrea del polígon que resulta de la unió dels dos anteriors^[7]. De manera que, si els tres enunciats són vàlids el Teorema de Pick queda demostrat.

Tots els polígons simple són triangulables

Per poder demostrar que tots els poligonals simples es poden triangular, ens imaginarem un polígon simple (P) de n vèrtexs. Doncs bé, ho demostrarem per inducció sobre n.

El primer pas de la inducció, per un polígon, és n= 3; en aquest cas el polígon ja és un triangle, amb això ja tenim el primer cas de la inducció demostrat.

Suposem ara, com a hipòtesi d'inducció, que el teorema és cert per a tots els polígons de n vèrtex i el demostrarem per a n+1 vèrtex.

Per poder demostrar-ho partim un polígon simple P de n+1 vèrtex i A un dels seus vèrtexs no sortints (Perquè un vèrtex sigui no sortint, hem de poder dibuixar una recta que passi pel mateix vèrtex i que a l'hora no talli cap altre vèrtex del polígon) i anomenem B i C als seus vèrtexs adjacents. Després dibuixem un segment des de B fins a C i l'anomenarem BC.

Una vegada plantejada aquesta situació ens podem trobar dos casos.

- En el primer cas el segment BC no talla cap vèrtex del polígon, de manera que divideix el polígon en dos polígons de n vèrtex o menys i aplicant la hipòtesi d'inducció el teorema queda demostrat^[5].

- En el segon cas el segment BC talla algun vèrtex del polígon o, més d'un, de manera que aquests vèrtex queden dins del triangle ABC. Llavors unirem el vèrtex A amb cadascun d'aquests punts i dibuixarem un altre segment, des del vèrtex A fins al vèrtex més proper a B que hagi quedat dins del triangle ABC, aquest vèrtex l'anomenarem D, aquest nou segment rebrà el nom de AD i separarà el polígon inicial en dos polígons amb menys de n vèrtex, de manera que podem aplicar la hipòtesi d'inducció a les seves parts^[8].

• 
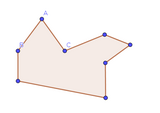  Polígon descrit en el primer cas.
• 
  Polígon descrit al primer cas dividit en dos pel segment BC.
• 
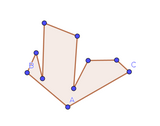  Polígon descrit en el segon cas.
• 
  Polígon descrit en el segon cas amb els segments BC i AD dibuixats.
• 
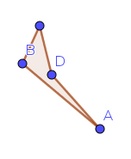  Un dels polígons resultants de dividir el polígon del segon cas amb el segment AD.
• 
  L'altre polígon resultant de dividir el polígon del segon cas amb el segment AD.

El Teorema és vàlid per a triangles reticulars

El Teorema és vàlid per a triangles amb els dos costats als eixos de coordenades^[6]

Si el triangle té els seus costats als eixos de coordenades aleshores tenim un triangle rectangle (T). Suposem que sigui amb base n i amb altura m i la seva hipotenusa té k punts frontera (sense comptar els extrems).

Amb això podem saber que la base té un total de n+1 punts frontera i l'altura m+1 punts frontera, aquestes dues dades ens permet saber que els punts frontera són ${\displaystyle B=m+1+n+1+k-1=m+n+k+1}$ (restem 1 perquè si no comptaríem el punt d'origen dos cops).

Per calcular els punts interiors ens caldrà fer un quadrat, simètric al triangle T respecte a la seva hipotenusa. Aquest quadrat tindrà un total de punts de ${\displaystyle T=(m+1)(n+1)}$i un total de punts frontera de ${\displaystyle B=2(m+1)+2(n+1)-4=2m+2n}$ (restem 4 per no comptar els vèrtexs dues vegades). Per tant, els seus punts interiors serà la resta dels punts totals menys els punts frontera, per tant ${\displaystyle mn-m-n+1}$^[9].

Això ens és útil saber-ho perquè així sabem que els punts interiors del rectangle simètric menys k són el doble de punts interiors del nostre triangle ${\displaystyle (m-1)(n-1)=mn-m-n+1}$, per tant, aquest nombre el dividim entre dos per obtenir els punts interiors del nostre triangle ${\displaystyle I={\frac {mn-m-n+1-k}{2}}}$.

Ara que ja sabem els punts interiors i els punts frontera, podem usar la fórmula de l'àrea del triangle, que és: ${\displaystyle {\frac {Base\times Altura}{2}}}$,^[10] que substituïda amb les nostres dades és ${\displaystyle {\frac {m\times n}{2}}}$, per veure si l'àrea del triangle A(T) és igual al resultat que obtindríem amb Pick P(T).

${\displaystyle P(T)=I+{\frac {B}{2}}-1}$

${\displaystyle I={\frac {mn-m-n+1-k}{2}}}$ ${\displaystyle B=m+n+k+1}$${\displaystyle P(T)={\frac {mn-m-n+1-k}{2}}+{\frac {m+n+k+1}{2}}-1}$

${\displaystyle P(T)={\frac {mn+2}{2}}-1}$

${\displaystyle P(T)={\frac {mn}{2}}}$

${\displaystyle P(T)=A(T)}$

Per tant, hem confirmat que en un triangle rectangle reticular, sí que es pot aplicar el Teorema de Pick.

• 
  Triangle de la demostració.
• 
  Rectangle creat pel triangle inicial i els seu simètric respecte a la hipotenusa.
• 
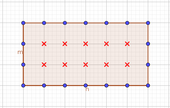  Rectangle resultant de negligir k.

El Teorema és vàlid per a un triangle amb un sol costat als eixos de coordenades^[6]

Per poder comprovar la validesa d'aquest enunciat ens caldrà imaginar un triangle on només els vèrtexs B i C estan situats en els eixos de coordenades. El nostre objectiu per poder demostrar aquest enunciat és comprovar que l'àrea del nostre triangle és igual al resultat de fer el Teorema de Pick, per tant A(ABC)=P(ABC).

Com ja sabem que l'àrea d'un triangle rectangle (amb els dos costats en els eixos), el que fem és construir un rectangle al voltant del triangle ABC. De manera que obtenim dos triangles rectangles (ADB i AEC) i un rectangle (ADCE), a més a més del triangle inicial (ABC), per tant sabem que l'àrea del rectangle serà la suma dels tres triangles. Així que...

${\displaystyle A(ADB)+A(ABC)+A(AEC)=A(ADCE)}$

${\displaystyle A(ADB)+A(ABC)+A(AEC)=P(ADCE)}$

${\displaystyle A(ADB)+A(ABC)+A(AEC)=P(ADB)+P(ABC)+P(AEC)}$

${\displaystyle A(ADB)+A(ABC)+A(AEC)=A(ADB)+P(ABC)+A(AEC)}$

SI cancel·lem els termes que es repeteixen a banda i banda de l'equació obtindrem

${\displaystyle A(ABC)=P(ABC)}$

Per tant, podem afirmar que el Teorema de Pick sí que és vàlid per a un triangle amb només un costat als eixos de coordenades.

• 
  Triangle amb només un costat sobre els eixos de coordenades.
• 
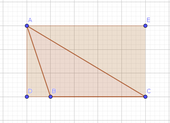  El resultant de dibuixar un rectangle sobre els vèrtex d'un triangle amb només un costat sobre els eixos de coordenades.

Triangle sense cap dels seus costats en els eixos de coordenades^[11]

La comprovació d'aquest enunciat segueix el mateix procediment que la de l'apartat anterior i el cas és quasi idèntic, només que en aquest hi ha la diferència de què quan representem un triangle sense cap costat en els eixos de coordenades i construïm el rectangle obtindrem tres triangles rectangles.

Per comprovar-ho gràficament seguirem el procediment que ja sabem.

${\displaystyle A(ADB)+A(ABC)+A(AEC)+A(BCF)=A(ADFE)}$

${\displaystyle A(ADB)+A(ABC)+A(AEC)+A(BCF)=P(ADFE)}$${\displaystyle A(ADB)+A(ABC)+A(AEC)+A(BCF)=A(ADB)+P(ABC)+A(AEC)+A(BCF)}$

Si cancel·lem els termes que es repeteixen a banda i banda de l'igualat obtindrem.

${\displaystyle A(ABC)=P(ABC)}$

Per tant podem confirmar que el tercer i darrer enunciat sobre tipus de triangles està demostrat, i com a conseqüència podem afirmar que podem calcular l'àrea de qualsevol mena de triangle reticular amb el Teorema de Pick

• 
  Triangle sense cap costat als eixos de coordenades.
• 
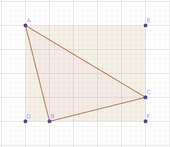  El resultant de dibuixar un rectangle sobre els vèrtex d'un triangle sense cap costat als eixos de coordenades.

El Teorema és vàlid per a dos polígons amb un costat comú^[7]

Per començar, plantejarem la següent situació: Tenim dos polígons ${\displaystyle P_{1}}$, els seus punts interiors seran ${\displaystyle I_{1}}$, els punts frontera ${\displaystyle B_{1}}$, i ${\displaystyle P_{2}}$, els seus punts interiors ${\displaystyle I_{2}}$ els punts frontera ${\displaystyle B_{2}}$. Aquests polígons comparteixen un costat el qual té un total de k punts en comú, i per tant, formen un gran polígon, anomenat ${\displaystyle P}$, els seus punts interiors seran ${\displaystyle I}$ i els seus punts frontera ${\displaystyle B}$.

Considerant l'àrea com a ${\displaystyle A(x)}$i Pick com a ${\displaystyle P(x)}$, i sabem que ${\displaystyle A(x)=P(x)}$.

El nostre objectiu és demostrar que ${\displaystyle P(P)=P(P_{1})+P(P_{2})}$. Per tant, substituirem la fórmula de Pick amb la terminologia que hem determinat prèviament.

${\displaystyle P(P)=I+{\frac {B}{2}}-1}$

${\displaystyle I=I_{1}+I_{2}+k-2}$ ${\displaystyle B=B_{1}+B_{2}-2k+2}$

${\displaystyle P(P)=I_{1}+I_{2}+k-2+{\frac {B_{1}+B_{2}-2k+2}{2}}-1}$

${\displaystyle P(P)=I_{1}+I_{2}+k-2+{\frac {B_{1}}{2}}+{\frac {B_{2}}{2}}-k+1}$

${\displaystyle P(P)=(I_{1}+{\frac {B_{1}}{2}}-1)+(I_{2}+{\frac {B_{2}}{2}}-1)}$

${\displaystyle P(P)=P(P_{1})+P(P_{2})}$

Per tant, després de veure aquest desenvolupament, podem afirmar que sí, que ${\displaystyle P(P)=P(P_{1})+P(P_{2})}$.

Després d'aquesta sèrie de demostracions el Teorema de Pick ha quedat demostrat, ja que si tots els polígons són triangulables, l'àrea de qualsevol triangle es pot calcular amb Pick i podem sumar els resultats dels diferents triangles que comparteixen costat, el Teorema de Pick queda provat per a qualsevol polígon reticular simple.

Com aplicar el Teorema

Ara que ja entenem el Teorema i sabem la seva demostració ens caldrà saber com aplicar-ho.

• 
  · Primer de tot, ens caldrà dibuixar una quadrícula.
• 
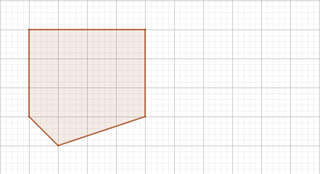  · Després dibuixarem el nostre polígon reticular simple asobre d'aquesta quadrícula.
• 
  · A continuació marcarem els punts frontera i els punts interiors del nostre polígon reticular simple.
• 
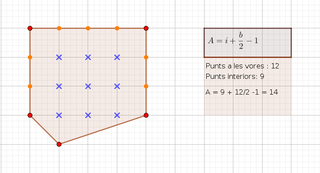  · Per últim, farem el recompte dels punts per poder utilitzar la fórmula i obtenir un resultat.${\displaystyle 9+{\frac {12}{2}}-1=14}$

Referències

Bibliografia

• Agfalvi, Mihaly; Kadar, Istvan; Papp, Erik. «Generalization of Pick's theorem for surface of polyhedra». A: Proceeding (en anglès). Scranton, Pennsylvania: ACM, 1999, p. 1-12. ISBN 1-58113-126-7. 
• Blatter, Christian. Another Pro of of Pick's Area Theorem (PDF) (en anglès) [Consulta: 11 novembre 2018].  Arxivat 12 August 2017^{[Date mismatch]} a Wayback Machine.
• Juanpere González, Àngel. Brunat, Josep M. (tutor). El Teorema de Pick. Barcelona: Universitat Politècnica de Catalunya, Facultat de Matemàtiques i Estadística, 2015 [Consulta: 11 novembre 2018]. 
• Pick, Georg «Geometrisches zur Zahlenlehre» (en alemany). Sitzungsberichte des Deutschen Naturwissenschaftlich-Medicinischen Vereines für Böhmen "Lotos" in Prag., V. 47, 1899, pàg. 311-319 [Consulta: 11 novembre 2018].
• Steinhaus, Hugo. Mathematical Snapshots (en anglès), 1969. ISBN 9780196317199. 
• Elduque, Alberto «Taller de Talento Matemático». El Teorema de Pick, 12-01-2007. Publicació sobre el Teorema de Pick de la Universitat de Saragossa
• El teorema de Pick, 25-10-2008. Publicació sobre el Teorema de Pick de la universitat de Granada