Cauchy-Folge

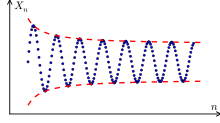
Eine Cauchy-Folge (bzw. Cauchyfolge), Cauchysche Folge oder Fundamentalfolge ist in der Mathematik eine Folge, bei der der Abstand der Folgenglieder im Verlauf der Folge beliebig klein wird. Cauchy-Folgen sind nach dem französischen Mathematiker Augustin-Louis Cauchy benannt und von grundlegender Bedeutung für den Aufbau der Analysis.

Eine Cauchy-Folge reeller Zahlen konvergiert immer und hat eine reelle Zahl als Grenzwert – der Grenzwert einer Cauchy-Folge rationaler Zahlen kann auch irrational sein. Die reellen Zahlen sind damit ein vollständiger Raum, da sie ein metrischer Raum sind und ein solcher definitionsgemäß genau dann vollständig ist, wenn in ihm alle Cauchy-Folgen konvergieren.

Cauchy-Folgen von Zahlen

Definition

Eine Folge ${\displaystyle (a_{i})_{i\in \mathbb {N} }}$ reeller Zahlen heißt Cauchy-Folge oder Fundamentalfolge, wenn es zu jedem ${\displaystyle \varepsilon >0}$ einen Index ${\displaystyle N}$ gibt, so dass ab diesem Index alle Folgenglieder weniger als ${\displaystyle \varepsilon }$ voneinander entfernt sind. Formal lässt sich diese Bedingung als

${\displaystyle \forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad \left|a_{m}-a_{n}\right|<\varepsilon }$

schreiben, wobei ${\displaystyle |\cdot |}$ den Betrag einer Zahl darstellt.

Anmerkungen

• In der Definition kann ${\displaystyle \geq N}$ auch durch ${\displaystyle >N}$ und ${\displaystyle <\varepsilon }$ auch durch ${\displaystyle \leq \varepsilon }$ ersetzt werden.

• Äquivalent zu dieser Definition kann man auch fordern, dass es zu jeder noch so kleinen positiven Zahl ${\displaystyle \varepsilon }$ ein Intervall der Länge ${\displaystyle 2\varepsilon }$ gibt, in dem fast alle Folgenglieder liegen.

• Diese Definition entspricht weitgehend der Definition für konvergente Folgen, ohne jedoch den Begriff des Grenzwertes einer Folge zu benutzen. Cauchy-Folgen wurden daher früher auch als „in sich konvergente Folgen“ oder „konzentrierte Folgen“ bezeichnet.

Beispiele

• Die Folge ${\displaystyle a_{i}={\tfrac {1}{i}}}$ ist eine Cauchy-Folge. Man kann nämlich zu einem beliebig vorgegebenen ${\displaystyle \varepsilon >0}$ ein ${\displaystyle N}$ so wählen, dass ${\displaystyle N>{\tfrac {1}{\varepsilon }}}$ erfüllt ist. Sind nun ${\displaystyle n\geq m>N}$ beliebig gewählt, dann gilt

${\displaystyle |a_{m}-a_{n}|=\left|{\frac {1}{m}}-{\frac {1}{n}}\right|=\left|{\frac {n-m}{mn}}\right|<{\frac {n}{mn}}={\frac {1}{m}}<{\frac {1}{N}}<\varepsilon }$.

• Die Folge ${\displaystyle a_{i}=i}$ ist keine Cauchy-Folge. Sei dazu ${\displaystyle \varepsilon ={\tfrac {1}{2}}}$ gewählt und ${\displaystyle N}$ eine beliebige natürliche Zahl. Dann kann man ${\displaystyle n=N+1}$ und ${\displaystyle m=n+1}$ wählen und es gilt immer^[1]

${\displaystyle |a_{m}-a_{n}|=|m-n|=1\geq \varepsilon }$.

Vollständigkeit

Es gibt Folgen rationaler Zahlen, deren Folgenglieder sich in der beschriebenen Weise häufen, ohne aber einen Grenzwert in der Menge der rationalen Zahlen zu haben. Ein Beispiel hierfür ist die Folge rationaler Zahlen mit der Bildungsvorschrift (siehe Heron-Verfahren)

${\displaystyle a_{1}:=1,\quad a_{i+1}:={\frac {a_{i}}{2}}+{\frac {1}{a_{i}}}}$.

Diese Folge ist eine Cauchy-Folge, sie besitzt aber als Grenzwert die irrationale Zahl ${\displaystyle {\sqrt {2}}}$ und konvergiert daher innerhalb der Menge der rationalen Zahlen nicht. Die Problematik, dass in der Menge der rationalen Zahlen ${\displaystyle \mathbb {Q} }$ viele Grenzwerte von Cauchy-Folgen nicht enthalten sind, führte zu der Idee der Vervollständigung des Zahlenbereichs auf die Menge ${\displaystyle \mathbb {R} }$ der reellen Zahlen.

Cauchy-Folgen in metrischen Räumen

Definition

Allgemeiner definiert man den Begriff der Cauchy-Folge für metrische Räume ${\displaystyle (X,d)}$, also beliebige Mengen ${\displaystyle X}$, auf denen eine Metrik ${\displaystyle d}$ gegeben ist. Eine Folge ${\displaystyle (x_{i})_{i\in \mathbb {N} }}$ von Elementen in ${\displaystyle X}$ heißt dann Cauchy-Folge, wenn

${\displaystyle \forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad d(x_{m},x_{n})<\varepsilon }$

gilt.^[2] Damit gibt es zu jedem reellen ${\displaystyle \varepsilon >0}$ einen Index ${\displaystyle N}$, so dass für alle natürlichen Zahlen ${\displaystyle m,n\geq N}$ der Abstand der entsprechenden Folgenglieder ${\displaystyle d(x_{m},x_{n})<\varepsilon }$ ist.

Eine dazu äquivalente geometrische Formulierung ist: Für jedes ${\displaystyle \varepsilon >0}$ gibt es einen Punkt ${\displaystyle a}$ und einen Index ${\displaystyle N}$, so dass alle Folgenglieder ab ${\displaystyle x_{N}}$ in der offenen Kugel ${\displaystyle B_{\varepsilon }(a)}$ um den Punkt ${\displaystyle a}$ mit Radius ${\displaystyle \varepsilon }$ liegen. Diese Version unterscheidet sich nur dadurch von der Konvergenzdefinition, dass hier der Mittelpunkt ${\displaystyle a}$ vom Radius ${\displaystyle \varepsilon }$ abhängen darf, während bei der Konvergenz der Grenzwert ${\displaystyle a}$ von ${\displaystyle \varepsilon }$ unabhängig sein muss.

Vollständigkeit

Jede konvergente Folge in einem metrischen Raum ist auch eine Cauchy-Folge. Konvergiert nämlich eine Folge ${\displaystyle (x_{i})_{i\in \mathbb {N} }}$ gegen einen Grenzwert ${\displaystyle x\in X}$, dann gibt es zu jedem ${\displaystyle \varepsilon >0}$ einen Index ${\displaystyle N\in \mathbb {N} }$, sodass ${\displaystyle d(x,x_{n})<{\tfrac {\varepsilon }{2}}}$ für alle ${\displaystyle n\geq N}$ gilt. Mit der Dreiecksungleichung für metrische Räume folgt dann für alle ${\displaystyle m,n\geq N}$

${\displaystyle d(x_{m},x_{n})\leq d(x_{m},x)+d(x,x_{n})<{\tfrac {\varepsilon }{2}}+{\tfrac {\varepsilon }{2}}=\varepsilon }$

und die Folge ist somit eine Cauchy-Folge. Die umgekehrte Richtung muss jedoch nicht notwendigerweise wahr sein, was letztendlich zur Einführung von vollständigen Räumen führte. In einem vollständigen Raum besitzt definitionsgemäß jede Cauchy-Folge einen Grenzwert und der Begriff der konvergenten Folge fällt mit dem Begriff der Cauchy-Folge zusammen. Jeder unvollständige metrische Raum kann jedoch durch die Bildung von Äquivalenzklassen von Cauchy-Folgen vervollständigt werden. Dabei werden zwei Cauchy-Folgen ${\displaystyle (x_{i})_{i\in \mathbb {N} }}$ und ${\displaystyle (y_{i})_{i\in \mathbb {N} }}$ von Elementen in ${\displaystyle X}$ als äquivalent angesehen, wenn

${\displaystyle \forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad d(x_{m},y_{n})<\varepsilon }$

oder, was dasselbe ist,

${\displaystyle \lim _{m,n\in \mathbb {N} }d(x_{m},y_{n})=0}$.

Liegt der Grenzwert einer der beiden Folgen in ${\displaystyle X}$, dann auch der der anderen, und die beiden Grenzwerte sind gleich.

Siehe auch

• Cauchy-Kriterium
• Cauchy-Netz

Weblinks

Literatur

• Konrad Königsberger: Analysis 1. Springer, Berlin 2004, ISBN 3-540-41282-4
• Konrad Königsberger: Analysis 2. Springer-Verlag, Berlin/Heidelberg, 2000, ISBN 3-540-43580-8
• Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg-Verlag, 8. Aufl. 2006, ISBN 3-528-67224-2

Einzelnachweise und Anmerkungen

1. ↑ Um einen Gegenbeweis zu führen, muss man die Definition umkehren: ${\displaystyle \exists \varepsilon >0~\forall N\in \mathbb {N} ~\exists m,n\geq N\colon \left|a_{m}-a_{n}\right|\geq \varepsilon }$.
2. ↑ Dirk Werner: Funktionalanalysis. 2005, S. 2.