RC-Glied
Unter RC-Gliedern versteht man in der Elektrotechnik Schaltungen, die aus einem ohmschen Widerstand (R – engl. resistor) und einem Kondensator (C – engl. capacitor) aufgebaut sind. RC-Glieder sind lineare, zeitinvariante Systeme. Im engeren Sinne sind damit die Filter wie der Tiefpass oder Hochpass gemeint. Bei einem Tiefpass, wie in nebenstehendem Bild, wird das Ausgangssignal am Kondensator abgegriffen, beim Hochpass dagegen am Widerstand.
Zum Potentialausgleich beziehungsweise bei der Funktionserdung finden sich Parallelschaltungen von Kondensator und Widerstand. Zur Begrenzung von elektromagnetischen Störungen finden sich Reihenschaltungen von Kondensator und Widerstand, wie beispielsweise bei dem Snubber.

Ue: Eingangsspannung
Ua: Ausgangsspannung
Verhalten im Zeitbereich
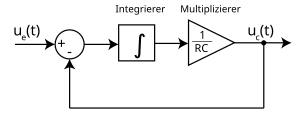
Allgemeine systemtheoretische Beschreibung des RC-Tiefpasses

Das RC-Glied in Tiefpasskonfiguration ist ein integrierendes, zeitkontinuierliches, lineares, zeitinvariantes Übertragungsglied. Die allgemeine systemtheoretische Beschreibung ergibt sich aus den Kirchhoffschen Regeln und den Strom-/Spannungs-Beziehungen an Kondensator bzw. Widerstand. Die Maschengleichung ergibt
- .
Da es sich um einen unverzweigten Stromkreis handelt, gilt . Für den Spannungsabfall am Widerstand gilt
und der Strom durch den Kondensator ist durch die Beziehung
festgelegt. Setzt man nun die Gleichung der Spannung über den Widerstand in die Maschengleichung ein, so erhält man
- .
Einsetzen des Stroms ergibt letztendlich die Differentialgleichung
- ,
welche das Übertragungsglied vollständig beschreibt: Das RC-Glied hat also ein proportionales Übertragungsverhalten mit Verzögerung 1. Ordnung und entspricht einem PT1-Glied mit der Zeitkonstante T = RC.
Um den integrierenden Charakter des Tiefpassfilters zu verdeutlichen, nehmen wir noch einige Umformungen vor. Die Gleichung wird auf beiden Seiten integriert
- ,
wobei sich Differential- und Integraloperator in einem Term direkt aufheben und folgt
- .
Umstellen nach der Ausgangsspannung ergibt letztendlich
- .
Die Integralgleichung im Zeitbereich kann direkt der Laplace-Transformation unterzogen werden, wodurch sich
ergibt. Durch Division des Ausgangssignals durch das Eingangssignal ergibt sich die Übertragungsfunktion des RC-Tiefpass:
- .
Durch Setzen von (mit der imaginären Einheit und der Kreisfrequenz ) ergibt sich die Fourier-Transformation und damit die spektrale Repräsentation des Systems:
- .
Die wohl wichtigste Klasse von Signalen zur Betrachtung des Filterverhaltens sind harmonische Signale, deshalb ist es häufig von großem Interesse, welches Dämpfungsverhalten das Filter auf ein Sinussignal hat. Durch das Eingangssignal

folgt in der zuvor hergeleiteten Differential- bzw. Integralgleichung dann
- .
Um die Ausgangsspannung zu finden, muss nach umgestellt werden, dies ist analytisch möglich. Es handelt sich um eine Lineare gewöhnliche Differentialgleichung, zu der es viele verschiedene Lösungsmethoden gibt. Betrachtet man die Anfangsbedingung , also den Fall, dass das System beim Einschwingen zunächst energielos ist, dann ergibt sich die Lösung zu
- .
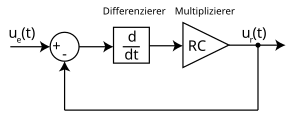
Allgemeine systemtheoretische Beschreibung des RC-Hochpasses

Auch beim RC-Hochpass handelt es sich um einen unverzweigten Stromkreis, hierbei wird die Ausgangsspannung jedoch am Widerstand abgegriffen. Systemtheoretisch handelt es sich um ein differenzierendes Übertragungsglied. Die Maschengleichung ergibt
- .
Für die Spannung über dem Kondensator gilt die Integralbeziehung
- .
Aufgrund der Unverzweigtheit des Stromkreises gilt , daraus folgt nach Einsetzen
- .
Der Strom im Integral lässt sich schreiben als: , eingesetzt in die Gleichung folgt
- ,
dabei handelt es sich um eine Integralgleichung, welche das System nun vollständig beschreibt. Um den differenzierenden Charakter des Hochpassfilters zu verdeutlichen, nehmen wir noch einige Umformungen vor. Die Gleichung wird auf beiden Seiten differenziert
- ,
wobei sich der Differential- und der Integraloperator wieder gegenseitig aufhebt
- .
Umstellen zur Ausgangsgröße ergibt dann
- ,
wodurch das differenzierende Verhalten offensichtlich wird. Die Gleichung kann der Laplace-Transformation unterzogen werden, wodurch
folgt. Durch Division des Ausgangssignals durch das Eingangssignal ergibt sich die Übertragungsfunktion des RC-Hochpasses:
Durch Setzen von ergibt sich die Fourier-Transformation und damit die spektrale Repräsentation des Systems:
- .
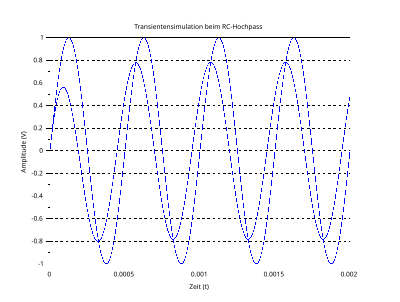
Auch hier betrachten wir wieder die Lösung der Differentialgleichung für ein harmonisches Eingangssignal, dazu kann die Laplace-Transformation genutzt werden. Das Eingangssignal sei
- ,
dessen Laplace-Transformierte lautet
- .
Einsetzen in die Übertragungsfunktion liefert
- .
Durch eine Umfangreiche Rücktransformation ergibt sich dann die Lösung der Differentialgleichung und damit das Transientenverhalten bei sinusförmigen Eingangssignal:
Ladevorgang
Exemplarisch ist hier die Systemantwort auf eine Sprungfunktion dargestellt. Angenommen, es liegt zunächst keine Spannung an und der Kondensator ist entladen (Q = 0). Ab dem Zeitpunkt t = 0 soll eine konstante Spannung Umax anliegen. Es fließt daraufhin ein Strom I(t), der den Kondensator auflädt. Mit der Ladung Q(t) im Kondensator wächst auch die am Kondensator anliegende Spannung UC(t)
bis maximal auf den Wert der angelegten äußeren Spannung, die deshalb hier Umax genannt wurde.
Für eine einfache Reihenschaltung teilt sich nach dem Maschensatz die Gesamtspannung auf die beiden Elemente, Kondensator und Ohmscher Widerstand, auf. Die Spannung am Widerstand ist demnach:
- .
Zum Zeitpunkt t = 0, wenn der Kondensator noch keine Ladung hat und daher keine Spannung trägt (UC = 0), liegt am Ohmschen Widerstand daher die volle Spannung an (UR = Umax) und wird mit zunehmender Aufladung des Kondensators geringer.
Nach dem ohmschen Gesetz ist der Strom proportional zur Spannung am Widerstand:
- .
Mit der sinkenden Spannung UR sinkt daher auch der Ladestrom I. Mit der Anfangsbedingung Q(0) = 0 hat die Differentialgleichung
die Lösung
- .

Entsprechend gilt für die Spannung am Kondensator:
- .
Die Ladezeit des Kondensators wird also durch das Produkt aus dem elektrischen Widerstand R und der Kapazität C des Kondensators bestimmt. Dieses Produkt nennt man die Zeitkonstante :
- .
Die Ladung und die Spannung am Kondensator wachsen zunächst stark und dann immer schwächer an und nähern sich asymptotisch ihrem Maximum. Theoretisch dauert es unendlich lange, bis UC(t) = Umax ist. Für praktische Zwecke kann man als Ladezeit
- .
verwenden. Der Kondensator ist dann fast vollständig (mehr als 99 %) geladen.
Die Zeitkonstante τ markiert zugleich den Zeitpunkt, an dem die am Beginn der Kurve angelegte Tangente den Endwert der Spannung erreicht. Der maximale Strom Imax = Umax/R fließt zum Zeitpunkt t = 0, wenn am Widerstand die volle Spannung Umax anliegt. Nach der Zeit τ wäre der Kondensator auf den Endwert geladen, wenn man ihn mit dem konstanten Strom Imax laden könnte.
Tatsächlich nimmt die Stromstärke bei konstanter angelegter Spannung jedoch mit der Zeit exponentiell ab:
- .
Nach der Zeit beträgt der Strom nur noch 1/e (≈37 %) seines Anfangswertes und nach der Zeit ist er auf weniger als 1 % abgefallen.
Entladevorgang
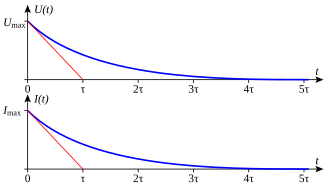
Umax ist die Anfangsspannung
Wenn der Kondensator zu Beginn auf den Wert Umax geladen ist und über den Widerstand R entladen wird, sind die Verhältnisse ähnlich. Da keine äußere Spannung anliegt, liegt am Kondensator betragsmäßig die gleiche Spannung wie am Widerstand:
- .
Dann sind Spannung, Ladung und Entladungsstrom zu Beginn am größten und fallen exponentiell ab:
Der Entladestrom ist bei der vorgegebenen Zählpfeilrichtung negativ.
Impulsantwort

Die Impulsantwort beschreibt den Ausgangsspannungsverlauf auf eine diracimpulsförmige Eingangsspannung. Der Ausgangsspannungsverlauf wird durch deren Zeitableitung beschrieben:
Dabei ist die momentane Spannung am Widerstand, die eine Umladung des Kondensators bewirkt. Der Spannungsimpuls wird durch das RC-Glied integriert und hinterlässt eine Kondensatorladung, die sich anschließend in Form einer e-Funktion entlädt.
Die Spannungsanstiegsgeschwindigkeit (Volt pro Sekunde) ist eine wichtige Größe in der Elektronik und Leistungselektronik.
Periodische Signale

Die Filterwirkung wird insbesondere bei Rechtecksignalen deutlich; die Filterantwort setzt sich aus Segmenten des Lade- und Entladeverhaltens zusammen. Die Flankensteilheit des Signals wird somit geringer (und damit die Anstiegszeit länger), dementsprechend werden im Frequenzspektrum die höheren Frequenzen stark gedämpft. RC-Glieder werden dementsprechend zur Entstörung und als Tiefpass eingesetzt.
Die Flankensteilheit der Spannung am Kondensator bei einer Amplitude U0 der Rechteck-Spannungsquelle sinkt vom unendlichen Wert der speisenden Rechteckspannung auf maximal
- .
ab. Der maximale Ladestrom (Spitzenstrom, Pulsstrom Ip) beträgt
- .
Diesen Strom müssen zum Beispiel mit einem RC-Entstörglied beschaltete Schaltkontakte oder Halbleiterschalter aushalten können.
Verhalten im Frequenzbereich
Tiefpass





Widerstand und Kondensator bilden einen frequenzabhängigen Spannungsteiler, der auch eine Phasenverschiebung von maximal (90°) bewirkt. Die Impedanzen sind bzw. . Für das RC-Glied gilt für eine harmonisch oszillierende Spannung der Frequenz :
und somit für das Übertragungsverhalten, das als Quotient von Ausgangs- zur Eingangsspannung definiert ist:
- ,
wobei die normierte Frequenz Ω = ω/ω0 sich aus der Division von Kreisfrequenz ω = 2πf und Grenz-Kreisfrequenz (Übergangsfrequenz, Eckfrequenz oder englisch cutoff frequency) ωc = 1/τ = 1/(RC) ergibt. Daraus ergibt sich die Grenzfrequenz fc, bei der Blindwiderstand und Widerstand den gleichen Wert annehmen, die Phasenverschiebung also (45°) und die Dämpfung etwa 3 dB beträgt:
Für tiefe Frequenzen Ω ≪ 1 ist H ungefähr 1, Ein- und Ausgangsspannung etwa gleich, weshalb man den Bereich auch engl. als Passband bezeichnet.
Für Frequenzen Ω ≫ 1 fällt H mit 20 dB pro Dekade = 6 dB pro Oktave ab. Der weggefilterte Bereich wird englisch mit Stopband bezeichnet.
Bei sehr tiefen Frequenzen, die deutlich kleiner als die Grenzfrequenz sind, fällt der Ladestrom des Kondensators nicht ins Gewicht und Eingangs- und Ausgangsspannung unterscheiden sich nur unmerklich. Die Phasenverschiebung beträgt annähernd 0°.
Steigt die Frequenz, dauert es – im Vergleich zur Schwingungsdauer – immer länger, bis der Kondensator auf die Eingangsspannung aufgeladen ist. Deshalb steigt die Phasenverschiebung.
Bei sehr hoher Frequenz strebt diese dem Grenzwert von 90° zu, allerdings wird dann die Spannung am Kondensator auch unmessbar klein.
Hochpass
Die Verschaltung als Hochpass unterscheidet sich von der des Tiefpasses durch Vertauschung von R und C. Demgemäß gilt
und
- ,
Der Amplitudengang ist gegenüber dem Tiefpass entlang Ω = 1 gespiegelt, hohe Frequenzen können nahezu ungedämpft passieren.
Beschreibung im Spektralbereich
Mit einer analogen Herleitung erhält man für den Tiefpass
- ,
eine Polstelle bei .
Bei dem Hochpass
- ,
ergibt sich ebenfalls eine Polstelle bei , zusätzlich eine Nullstelle im Ursprung. Das RC-Glied stellt damit einen Butterworth-Filter 1. Ordnung dar.
Weblinks
- Interaktive Darstellung des zeitlichen Verlaufs von Lade- und Entladevorgang. In: GeoGebra. Abgerufen am 5. Januar 2021
- RC-Glied Berechnung Übergangsfrequenz und Zeitkonstante
- @1@2Vorlage:Toter Link/schulen.eduhi.atAnimation zum Auf- und Entladen des Kondensators (Seite nicht mehr abrufbar, festgestellt im Juli 2023. Suche in Webarchiven)













































































