Strahlensatz

Der Strahlensatz (man spricht auch vom ersten und zweiten Strahlensatz) oder Vierstreckensatz gehört zu den wichtigsten Aussagen der Elementargeometrie. Er befasst sich mit den Streckenverhältnissen, die entstehen, wenn zwei von einem gemeinsamen Punkt ausgehende Strahlen von einem Parallelenpaar geschnitten werden. Seine Aussagen ermöglichen es bei vielen geometrischen Überlegungen, unbekannte Streckenlängen auszurechnen. Traditionell wird der Strahlensatz dem griechischen Mathematiker Thales zugeschrieben, weshalb er außerhalb des deutschen Sprachraums oft auch als Satz des Thales bezeichnet wird.

In der synthetischen Geometrie können die ersten beiden Strahlensätze mit Einschränkungen sinngemäß auf affine Translationsebenen verallgemeinert werden und gelten uneingeschränkt für desarguesche Ebenen. Dagegen gilt der dritte Strahlensatz, der in der synthetischen Geometrie auch Dreistrahlsatz genannt wird, im Allgemeinen nur für pappussche Ebenen, siehe dazu Affine Translationsebene – Strahlensatz und Streckungen.

Formulierung der Strahlensätze

Wenn zwei von einem gemeinsamen Punkt ${\displaystyle Z}$ ausgehende Strahlen von zwei Parallelen geschnitten werden, die nicht durch den Ausgangspunkt ${\displaystyle Z}$ gehen, dann gelten die folgenden Aussagen:^[1][2]

1. Es verhalten sich je zwei Abschnitte auf der einen Geraden so zueinander wie die ihnen entsprechenden Abschnitte auf der anderen Geraden, also zum Beispiel ${\displaystyle {\frac {|ZA|}{|AA^{\prime }|}}={\frac {|ZB|}{|BB^{\prime }|}}}$, ${\displaystyle {\frac {|ZA|}{|ZA^{\prime }|}}={\frac {|ZB|}{|ZB^{\prime }|}}}$ oder ${\displaystyle {\frac {|AA^{\prime }|}{|ZA^{\prime }|}}={\frac {|BB^{\prime }|}{|ZB^{\prime }|}}}$
2. Es verhalten sich die Abschnitte auf den Parallelen wie die ihnen entsprechenden, vom Scheitel aus gemessenen Strecken auf jeweils derselben Geraden:${\displaystyle {\frac {|AB|}{|A^{\prime }B^{\prime }|}}={\frac {|ZA|}{|ZA^{\prime }|}}={\frac {|ZB|}{|ZB^{\prime }|}}}$.

Der erste Strahlensatz bezieht sich also auf die Verhältnisse von Strahlenabschnitten und der zweite auf die Verhältnisse von Strahlen- und Parallelenabschnitten.

Bemerkung (Umkehrung des 1. Strahlensatzes):^[1]

Ist Eigenschaft 1 erfüllt, so kann man auf parallele Geraden schließen. Ist dagegen Eigenschaft 2 gegeben, so ist ein entsprechender Schluss auf Parallelität nicht möglich.

Erweiterungen

Der erste und zweite Strahlensatz gelten auch, wenn man die beiden Strahlen mit gemeinsamen Ausgangspunkt ${\displaystyle Z}$ durch zwei Geraden, die sich in ${\displaystyle Z}$ schneiden, ersetzt. Liegt der Schnittpunkt ${\displaystyle Z}$ auf derselben Seite der beiden Parallelen („V-Figur“), so liegt die Situation des Strahlensatzes vor. Liegt ${\displaystyle Z}$ zwischen den beiden Parallelen („X-Figur“), so gelten aber weiterhin die für den Strahlensatz formulierten Streckenverhältnisse, da man diese Konfiguration („X-Figur“) durch eine Punktspiegelung in ${\displaystyle Z}$ in eine Strahlensatzkonfiguration („V-Figur“) mit den gleichen Streckenlängen überführen kann.^[2] Allerdings ist die Umkehrung des ersten Strahlensatzes nicht mehr möglich, wenn man ihn mit Geraden anstatt mit Strahlen formuliert.^[3]

Betrachtet man mehr als zwei Geraden, die sich in einem Punkt ${\displaystyle Z}$ schneiden, so erhält man auch Aussagen über die zusätzlichen auf den Parallelen entstandenen Strecken. Es stehen je zwei Abschnitte auf den Parallelen, die einander entsprechen, in gleichem Verhältnis zueinander. Schneidet zum Beispiel eine dritte Gerade die Parallelen in ${\displaystyle C}$ und ${\displaystyle C^{\prime }}$ (siehe Zeichnung) so gilt das folgende Streckenverhältnis:

${\displaystyle {\frac {|BC|}{|AC|}}={\frac {|B^{\prime }C^{\prime }|}{|A^{\prime }C^{\prime }|}}}$.

Verwandte geometrische Konzepte

Der Strahlensatz steht in engem Zusammenhang mit dem Begriff der geometrischen Ähnlichkeit. Die Dreiecke ${\displaystyle ZAB}$ und ${\displaystyle ZA^{\prime }B^{\prime }}$ sind in jeder der drei Skizzen sowie ${\displaystyle ZAC}$ und ${\displaystyle ZA^{\prime }C^{\prime }}$ in der Skizze nach Satz 3 (in „Erweiterungen“) zueinander ähnlich. Dies bedeutet insbesondere, dass entsprechende Seitenverhältnisse in diesen Dreiecken übereinstimmen – eine Aussage, aus der sich unmittelbar der Strahlensatz ergibt.

Siehe auch: Ähnlichkeitssätze

Ein weiteres Konzept, das mit dem Strahlensatz zusammenhängt, ist das der zentrischen Streckung (einer speziellen geometrischen Abbildung). In den angesprochenen drei Skizzen bildet die erste (V-Figur) beispielsweise die zentrische Streckung mit Zentrum ${\displaystyle Z}$ und Streckungsfaktor (Abbildungsfaktor) ${\displaystyle 1{,}5}$ die Punkte ${\displaystyle A}$ und ${\displaystyle B}$ auf die Punkte ${\displaystyle A^{\prime }}$ bzw. ${\displaystyle B^{\prime }}$ ab. Entsprechendes gilt für die zweite Skizze (X-Figur); hier ist der Streckungsfaktor gleich ${\displaystyle -0{,}5.}$

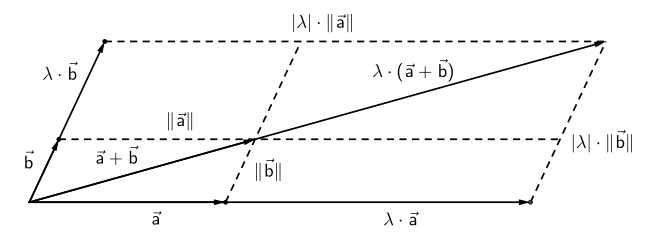
Eine ähnlich enge Beziehung besteht zur Vektorrechnung. Die Rechenregel

${\displaystyle \lambda \left({\vec {a}}+{\vec {b}}\right)=\lambda {\vec {a}}+\lambda {\vec {b}}}$

für zwei Vektoren ${\displaystyle {\vec {a}},{\vec {b}}}$ und einen reellen Skalar ${\displaystyle \lambda }$ ist nur eine andere Ausdrucksweise für den Strahlensatz, denn es gilt dann:

${\displaystyle {\frac {\|\lambda \cdot {\vec {a}}\|}{\|{\vec {a}}\|}}={\frac {\|\lambda \cdot {\vec {b}}\|}{\|{\vec {b}}\|}}={\frac {\|\lambda \cdot ({\vec {a}}+{\vec {b}})\|}{\|{\vec {a}}+{\vec {b}}\|}}=|\lambda |}$.

Hierbei bezeichnet ${\displaystyle \|{\vec {x}}\|}$ die Länge (euklidische Norm) des Vektors ${\displaystyle {\vec {x}}}$

Anwendungen

Vermessung

In der Verhältnisgleichung des Strahlensatz bestimmen drei (bekannte) Größen die (möglicherweise unbekannte) vierte Größe. Dies lässt sich in der Vermessung von unzugänglichen, nicht direkt messbaren Strecken verwenden, indem man die nicht direkt messbare Strecke als (unbekannte) vierte Größe in einer Strahlensatzkonfigurationen wählt. Einfache Messgeräte, die auf diesem Prinzip beruhen, sind der Jakobsstab und das Försterdreieck. Auch der Daumensprung zum Schätzen von Entfernungen beruht auf diesem Prinzip.

Höhe der Cheops-Pyramide

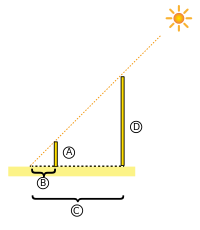
Ein einfaches Beispiel für die Anwendung des Strahlensatzes soll auf den antiken griechischen Philosophen und Mathematiker Thales von Milet zurückgehen. Dieser habe mit Hilfe eines Stabes durch Messung der Schattenlänge die Höhe der ägyptischen Cheopspyramide ermittelt. In anderen Sprachen wird der Strahlensatz daher oft auch als Satz des Thales^[4] bezeichnet.

Die folgende Beispielrechnung ermittelt die Höhe der Cheopspyramide mit Hilfe des zweiten Strahlensatzes, sie entspricht jedoch vermutlich nicht der exakten Berechnung des Thales selbst^[5]:

Zunächst bestimmt man die Seitenlänge der Pyramide und anschließend die Länge des Schattens ebenjener. Anschließend steckt man einen Stab senkrecht in den Boden und vermisst dessen Höhe und dessen Schattenlänge. Man erhält dann die folgenden Werte:

• Höhe des Stabes: ${\displaystyle A=1{,}63\,\mathrm {m} }$
• Schattenlänge des Stabes: ${\displaystyle B=2{,}00\,\mathrm {m} }$
• Direkt messbare Schattenlänge der Pyramide: ${\displaystyle 65\,\mathrm {m} }$
• Seitenlänge der Pyramide: ${\displaystyle 230\,\mathrm {m} }$
• Gesamte Schattenlänge der Pyramide: ${\displaystyle C=65\,\mathrm {m} +{\tfrac {1}{2}}\cdot 230\,\mathrm {m} }$
• Gesuchte Höhe der Pyramide: ${\displaystyle D}$

Mit Hilfe des Strahlensatzes (Skizze 2) stellt man die folgende Gleichung auf:

${\displaystyle {\frac {D}{A}}={\frac {C}{B}}}$

Die Länge der Seite ${\displaystyle C}$ des Dreiecks setzt sich dabei aus der halben Seitenlänge und der Länge des Schattens der Pyramide zusammen. Umgestellt nach D erhielt man:

${\displaystyle D={\frac {A\cdot C}{B}}={\frac {1{,}63\,\mathrm {m} \cdot \left(65\,\mathrm {m} +{\frac {1}{2}}\cdot 230\,\mathrm {m} \right)}{2{,}00\,\mathrm {m} }}={\frac {1{,}63\,\mathrm {m} \cdot 180\,\mathrm {m} }{2{,}00\,\mathrm {m} }}={\underline {146{,}7\,\mathrm {m} }}}$

Flussbreite

Auch in der Landvermessung kann der Strahlensatz verwendet werden, um die Länge schwer zugänglicher Strecken wie zum Beispiel die Entfernung gegenüberliegender Ufer von Gewässern zu bestimmen. Die Breite eines Flusses (siehe Grafik rechts) kann man wie folgt bestimmen. Zunächst markiert man die Endpunkte A und B der zu bestimmenden Strecke, dann konstruiert man eine zu AB rechtwinklige AC. Eine solche Konstruktion kann man zum Beispiel mit Hilfe eines Drehkreuzes, Winkelspiegels oder Doppelpentagonprisma durchführen. Auf AC wählt man einen (beliebigen) Punkt E von dem man aus den Punkt B am anderen Ufer anpeilt und die Strecke EB dann über E hinaus in die entgegengesetzte Richtung verlängert. Dann konstruiert man im Punkt C eine zu AC rechtwinklige Strecke, die die Verlängerung von EB im Punkt D schneidet. Da die Strecken AE, CE und CD alle auf derselben Uferseite liegen, lassen sie sich einfach vermessen und der zweite Strahlensatz liefert dann die gesuchte Flussbreite:

${\displaystyle |AB|={\frac {|AE|\cdot |CD|}{|CE|}}}$

Teilung einer Strecke

Der erste Strahlensatz ermöglicht, mit einem einfachen Verfahren – ohne Berechnungen oder Messungen – eine Strecke in einem (ganzzahligen) Verhältnis ${\displaystyle m:n}$ (${\displaystyle n,m\in \mathbb {N} }$) zu teilen.^[2] Zu einer gegebenen Strecke AB zeichnet man einen Strahl mit Startpunkt in A ein. Dann trägt man auf dem Strahl beginnend an A m+n gleich lange und aufeinander folgende Strecken ab. Den Endpunkt der m+n-ten Strecke verbindet man mit B und zeichnet dann die Parallele zu dieser Strecke durch den Endpunkt der m-ten Strecke. Diese Parallele teilt die Strecke AB im gewünschten Verhältnis ${\displaystyle m:n}$.

Weitere Anwendungen und Verallgemeinerungen

• Zentrische Streckungen und damit das Skalieren von Grafiken.
• In der Strahlenoptik beschreiben die Strahlensätze die Vergrößerungsverhältnisse bei einer Lochkamera und – zusammen mit der Linsengleichung – bei einer fehlerfreien dünnen Linse.
• Die Aussagen des ersten und zweiten Strahlensatzes können in der synthetischen Geometrie auf bestimmte nichtdesarguesche Ebenen, die affinen Translationsebenen, verallgemeinert werden.
• Konstruktion einer Dezimalzahl als praktisches Anwendungsbeispiel des dritten Strahlensatzes in Kombination mit Zahlenstrahlen
• Multiplikation mit Zirkel und Lineal
• Division mit Zirkel und Lineal
• Potenz mit Zirkel und Lineal

Beweis

Die in Satz 1 aufgestellten Streckenverhältnisse lassen sich über flächengleiche Dreiecke in der Strahlensatzfigur herleiten. Die Sätze 2 und 3 sowie die Umkehrung von Satz 1 ergeben sich dann durch die Anwendung von Satz 1 bzw. der schon bewiesenen Sätze.

Satz 1

Die Lote von A' bzw. B' auf die Gerade ${\displaystyle AB}$ haben die gleiche Länge, da ${\displaystyle AB}$ parallel zu ${\displaystyle A'B'}$ ist. Diese Lote sind Höhen der Dreiecke ABB' bzw. ABA', welche die zugehörige Grundseite ${\displaystyle [AB]}$ gemeinsam haben. Für die Flächen gilt daher^[1]

${\displaystyle |\triangle ABB'|=|\triangle ABA'|}$

und weiter

${\displaystyle |\triangle ABB'|+|\triangle ZBA|=|\triangle ABA'|+|\triangle ZBA|}$

oder flächenvereint

${\displaystyle |\triangle ZB'A|=|\triangle ZBA'|}$.

Aus der ersten Zeile folgt:

${\displaystyle {\frac {|\triangle ZBA|}{|\triangle ABB'|}}={\frac {|\triangle ZBA|}{|\triangle ABA'|}}}$

und aus der zweiten:

${\displaystyle {\frac {|\triangle ZBA|}{|\triangle ZB'A|}}={\frac {|\triangle ZBA|}{|\triangle ZBA'|}}}$

Das Anwenden der Standardformel zur Flächenberechnung von Dreiecken (${\displaystyle {\tfrac {g\cdot h}{2}}}$) liefert dann

${\displaystyle {\frac {|ZB|\cdot |AF|}{|BB'|\cdot |AF|}}={\frac {|ZA|\cdot |EB|}{|AA'|\cdot |EB|}}}$ und ${\displaystyle {\frac {|ZB|\cdot |AF|}{|ZB'|\cdot |AF|}}={\frac {|ZA|\cdot |EB|}{|ZA'|\cdot |EB|}}}$

Kürzen liefert die ersten beiden Gleichungen aus Satz 1

${\displaystyle {\frac {|ZB|}{|BB'|}}={\frac {|ZA|}{|AA'|}}}$ und ${\displaystyle {\frac {|ZB|}{|ZB'|}}={\frac {|ZA|}{|ZA'|}}}$.

Aus der letzten Gleichung erhält man dann

${\displaystyle 1-{\frac {|ZB|}{|ZB'|}}=1-{\frac {|ZA|}{|ZA'|}}}$

Nun bringt man auf beiden Seiten den jeweiligen Ausdruck auf den gleichen Nenner

${\displaystyle {\frac {|ZB'|-|ZB|}{|ZB'|}}={\frac {|ZA'|-|ZA|}{|ZA'|}}}$

und dies entspricht dann der dritten Gleichung aus Satz 1

${\displaystyle {\frac {|BB'|}{|ZB'|}}={\frac {|AA'|}{|ZA'|}}}$

Satz 1 – Beweis nach Archimedes

Archimedes reichte es, die Gleichheit zweier Seitenverhältnisse für einen Fall nachzuweisen. Die anderen Fälle ergeben sich daraus unmittelbar.

Der Beweis wird nicht zitiert, sondern lediglich gemäß der Archimedischen Methodenlehre^[6] ausgeführt. Mit den üblichen Seiten- und Winkelbezeichnungen für die Dreiecke ${\displaystyle ABZ}$ und ${\displaystyle A'B'Z}$ (siehe nebenstehende Skizze) wird gezeigt, dass ${\displaystyle {\frac {a}{a^{\prime }}}={\frac {b}{b^{\prime }}}}$ (entspricht ${\displaystyle {\tfrac {\overline {BZ}}{\overline {B'Z}}}={\tfrac {\overline {AZ}}{\overline {A'Z}}}}$) gilt. Die Winkel ${\displaystyle \alpha }$ und ${\displaystyle \alpha }$' sowie ${\displaystyle \beta }$ und ${\displaystyle \beta }$' sind als Stufenwinkel gleich.

Vorgehensweise

Bezeichne die Höhen, die durch das Lot von ${\displaystyle Z}$ auf die Geraden gegeben sind, mit ${\displaystyle h}$ und ${\displaystyle h'}$ sowie deren Fußpunkte mit ${\displaystyle H}$ und ${\displaystyle H'}$. Da ${\displaystyle \alpha }$ gleich ${\displaystyle \alpha }$' ist, haben jeweils die „ferne“ Kathete und die Hypotenuse in beiden rechtwinkligen Dreiecken ${\displaystyle AHZ}$ und ${\displaystyle A'H'Z}$ dasselbe Verhältnis zueinander. (In „moderner“ Formulierung: ${\displaystyle \sin(\alpha )}$ gleich Gegenkathete von ${\displaystyle \alpha }$ zu Hypotenuse).

Demzufolge gilt

${\displaystyle {\frac {h}{b}}={\frac {h^{\prime }}{b^{\prime }}}}$ und daher ${\displaystyle {\frac {h}{h^{\prime }}}={\frac {b}{b^{\prime }}}}$.

Aus ${\displaystyle \beta }$ gleich ${\displaystyle \beta }$' folgen durch entsprechende Betrachtung der Dreiecke ${\displaystyle HBZ}$ und ${\displaystyle H'B'Z}$ die Gleichungen

${\displaystyle {\frac {h}{a}}={\frac {h^{\prime }}{a^{\prime }}}}$ bzw. ${\displaystyle {\frac {h}{h^{\prime }}}={\frac {a}{a^{\prime }}}}$.

Und schließlich

${\displaystyle {\frac {a}{a^{\prime }}}={\frac {b}{b^{\prime }}}}$.

Was zu beweisen war.

Satz 2

Der Satz 2 ist die konstruktive Erweiterung von Satz 1.^[1]

Konstruiere eine Parallele zu ${\displaystyle ZB'}$ durch ${\displaystyle A}$. Diese Parallele schneidet ${\displaystyle A'B'}$ in ${\displaystyle G}$.

Wegen ${\displaystyle |AB|=|B'G|}$ gilt aufgrund von Satz 1:

${\displaystyle {\frac {|ZA|}{|ZA'|}}={\frac {|B'G|}{|A'B'|}}}$ worin sich ${\displaystyle |B'G|}$ durch ${\displaystyle |AB|}$ ersetzen lässt: ${\displaystyle {\frac {|ZA|}{|ZA'|}}={\frac {|AB|}{|A'B'|}}}$

Umkehrung von Satz 1

Angenommen ${\displaystyle AB}$ und ${\displaystyle A'B'}$ wären nicht parallel. Dann gibt es eine Parallele zu ${\displaystyle AB}$, die durch den Punkt ${\displaystyle B'}$ geht und den Strahl ${\displaystyle ZA}$ in ${\displaystyle A'_{0}\neq A'}$ (*) schneidet. Da nach Voraussetzung ${\displaystyle {\tfrac {|ZA'|}{|ZA|}}={\tfrac {|ZB'|}{|ZB|}}}$ gilt, ergibt sich

${\displaystyle |ZA'|={\frac {|ZB'|\cdot |ZA|}{|ZB|}}}$

Andererseits gilt nach dem ersten Strahlensatz auch

${\displaystyle |ZA'_{0}|={\frac {|ZB'|\cdot |ZA|}{|ZB|}}}$.

Dies bedeutet, dass ${\displaystyle A'}$ und ${\displaystyle A'_{0}}$ beide auf dem Strahl ${\displaystyle ZA}$ liegen und den gleichen Abstand von ${\displaystyle Z}$ haben. Damit sind die beiden Punkte jedoch identisch, also ${\displaystyle A'=A'_{0}}$. Dies ist ein Widerspruch dazu, dass es sich nach Bedingung (*) um 2 verschiedene Punkte handeln soll. Also führt die Annahme der Nichtparallelität zu einem Widerspruch und kann daher nicht richtig sein; oder anders ausgedrückt: Es muss ${\displaystyle AB\parallel A'B'}$ gelten.^[1]

Mehr als zwei Geraden

Satz 2 lässt sich zu Aussagen über drei oder mehr Geraden erweitern.

Ziehe eine Gerade durch ${\displaystyle Z}$ und ${\displaystyle AB}$, dabei ergeben sich die Schnittpunkte ${\displaystyle C}$ auf ${\displaystyle AB}$ sowie ${\displaystyle C'}$ auf ${\displaystyle A'B'}$. Konstruiere eine Parallele zu ${\displaystyle ZB'}$ durch ${\displaystyle C}$, die ${\displaystyle A'B'}$ in ${\displaystyle G'}$ schneidet.

Wegen ${\displaystyle |AB|=|B'G|}$ und ${\displaystyle |BC|=|B'G'|}$ gilt aufgrund von Satz 2:

${\displaystyle {\frac {|BC|}{|B'C'|}}={\frac {|ZC|}{|ZC'|}}={\frac {|CA|}{|C'A'|}}}$

Also hat man ${\displaystyle {\tfrac {|BC|}{|B'C'|}}={\tfrac {|CA|}{|C'A'|}}}$ oder umgestellt auch ${\displaystyle {\tfrac {|BC|}{|CA|}}={\tfrac {|B'C'|}{|C'A'|}}}$.

Literatur

• Wendelin Degen, Lothar Profke: Grundlagen der affinen und euklidischen Geometrie. Teubner, Stuttgart 1976, ISBN 3-519-02751-8.
• Lorenz Halbeisen, Norbert Hungerbühler, Juan Läuchli: Mit harmonischen Verhältnissen zu Kegelschnitten: Perlen der klassischen Geometrie. Springer 2016, ISBN 9783662530344, S. 191–208.
• Hans Schupp: Elementargeometrie. Schöningh, Paderborn 1977, ISBN 3-506-99189-2, S. 124 ff. (Uni-Taschenbücher 669 Mathematik).
• Siegfried Krauter, Christine Bescherer: Erlebnis Elementargeometrie. Springer Spektrum, 2-te Auflage 2013, ISBN 978-3-8274-3025-0, S. 147–157
• Franz Lemmermeyer: Mathematik à la Carte. Springer Spektrum, 2015, ISBN 978-3-662-45269-1, S. 118–122
• Manfred Leppig (Hrsg.): Lernstufen Mathematik. 1. Auflage, 4. Druck. Girardet, Essen 1981, ISBN 3-7736-2005-5, S. 157–170.
• Hartmut Wellstein, Peter Kirsche: Elementargeometrie. Eine aufgabenorientierte Einführung. Vieweg+Teubner Verlag 2009, ISBN 978-3-8348-0856-1, S. 36–41

Weblinks

• Symmetrie und Ähnlichkeit, Strahlensätze – Sinusmaterialien zum Strahlensatz (pdf)
• Alexander Bogomolny: Thales' Theorems und insbesondere Thales' Theorem auf cut-the-knot.org
• Strahlensatz interaktiv
• Euklid's Elements 6. Buch, L.2 engl.

Einzelnachweise

1. ↑ ^{a b c d e} Hans Schupp: Elementargeometrie. Schöningh, Paderborn 1977, ISBN 3-506-99189-2, S. 124 ff. (Uni-Taschenbücher 669 Mathematik).
2. ↑ ^{a b c} Strahlensätze. In: Schülerduden: Mathematik I. Dudenverlag, 8. Auflage, Mannheim 2008, S. 431–433
3. ↑ Ilka Agricola, Thomas Friedrich: Elementargeometrie. Springer Spektrum, 4-te Auflage 2015, ISBN 978-3-658-06730-4, S. 1–4
4. ↑ Nicht zu verwechseln mit dem im deutschen Sprachraum als Satz des Thales bezeichneten Spezialfall des Kreiswinkelsatzes.
5. ↑ Von Thales selbst sind keine Werke erhalten geblieben. Es gibt jedoch mehrere historische Quellen, die die Berechnung der Pyramidenhöhe durch Thales erwähnen. Alle diese Quellen sind aber mehrere Jahrhunderte nach dem Tode Thales verfasst worden und leicht unterschiedlich in ihrer Beschreibung, so dass sich letztendlich nicht mit Bestimmtheit sagen lässt, inwieweit Thales den Strahlensatz selbst oder einen Spezialfall von ihm als geometrischen Lehrsatz kannte oder ob er lediglich eine physikalische Beobachtung anwandte. So steht bei Diogenes Laertius: "Hieronymus sagt, dass es Thales sogar gelang die Höhe der Pyramiden zu bestimmen, indem er den Schatten der Pyramide genau in dem Augenblick vermass, in dem seine eigene Schattenlänge seiner Körpergröße entsprach." Eine ähnliche Formulierung findet man bei Plinius: "Thales entdeckte, wie man die Höhe von Pyramiden und anderen Objekten bestimmt, nämlich indem man den Schatten des Objektes genau zu dem Zeitpunkt misst, an dem Höhe und Schatten gleich lang sind." Bei Plutarch jedoch findet sich eine Beschreibung, die eventuell eine Kenntnis des Strahlensatzes vermuten lässt: "… ohne Schwierigkeiten und Zuhilfenahme eines Instrumentes, stellte er lediglich einen Stock am Ende des Pyramidenschatten auf und erhielt so zwei durch die Sonnenstrahlen erzeugte Dreiecke … dann zeigte er, dass die Höhe des Stocks und die Höhe der Pyramide im selben Verhältnis stehen, wie die Schattenlänge des Stockes und die Schattenlänge der Pyramide" (Quelle: Biographie des Thales im MacTutor)
6. ↑ Archimedes Werke. Übersetzt und mit Anmerkungen versehen von Arthur Czwalina Wiss. Buchgesellschaft, Darmstadt 1983, ISBN 3-534-02029-4