Zentrierte Fünfeckszahl

Die zentrierten Fünfeckszahlen gehören zu den zentrierten Polygonalzahlen, das heißt, es sind zweidimensionale figurierte Zahlen. Sie beziffern die Anzahl von Steinen, mit denen es möglich ist, ein Fünfeck wie in nebenstehendem Schema auszulegen.

Konstruktion

Es liegt ein Stein in der Mitte und um diesen werden dann schrittweise weitere Steine gelegt, und zwar nacheinander 5, 10, 15 usw., sodass ein Fünfeck entsteht.

Die ersten zentrierten Fünfeckszahlen sind

1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, … (Folge A005891 in OEIS)

Bei manchen Autoren zählt die 0 auch noch als nullte figurierte Zahl dazu.

Berechnung

Die n {\displaystyle n} -te zentrierte Fünfeckzahl ist

5 ⋅ ( n − 1 ) 2 + 5 ⋅ ( n − 1 ) + 2 2 = 5 n 2 − 5 n + 2 2 , {\displaystyle {\frac {5\cdot (n-1)^{2}+5\cdot (n-1)+2}{2}}={\frac {5n^{2}-5n+2}{2}},}

falls man 1 als erste zentrierte Fünfeckszahl definiert.

Weiteres

Erzeugende Funktion

Die Folge der zentrierten Fünfeckszahlen haben eine erzeugende Funktion, nämlich

x 2 + 3 x + 1 ( 1 − x ) 3 = 1 + 6 x + 16 x 2 + 31 x 3 + 51 x 4 + … {\displaystyle {\frac {x^{2}+3x+1}{(1-x)^{3}}}=\mathbf {1} +\mathbf {6} x+\mathbf {16} x^{2}+\mathbf {31} x^{3}+\mathbf {51} x^{4}+\ldots }

Verwandte figurierte Zahlen

  • Die (dezentralen) Fünfeckszahlen beziehen sich auf eine andere Möglichkeit, Steine zu Fünfecken auszulegen:
  • Die vierte dezentrale Fünfeckszahl 22.
    Die vierte dezentrale Fünfeckszahl 22.
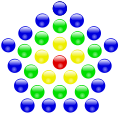
  • Die vierte zentrierte Fünfeckszahl 31.
    Die vierte zentrierte Fünfeckszahl 31.
    • Legt man nach diesem Muster keine Fünfecke, sondern Drei-, Vier- oder Sechsecke, erhält man die anderen zentrierten Polygonalzahlen oder Polygonalzahlen.

    Siehe auch

    • Figurierte Zahl
    • Fünfeckszahl

    Weblinks

    • Eric W. Weisstein: Centered Polygonal Numbers auf MathWorld.