Kosinuaren teorema

Trigonometrian, kosinuaren teorema^[1], triangelu zuzenetarako Pitagorasen teoremaren orokortze bat da. Teoremak triangelu baten edozein alde beste biekin eta bi alde horiek osatzen duten angeluaren kosinuarekin erlazionatzen du:

Kosinuaren teorema

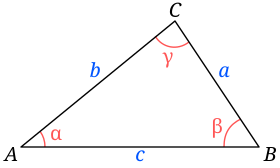
Izan bedi edozein ABC triangelu, non α, β eta γ bere angeluak diren eta a, b eta c angelu horien aurkako aldeak. Orduan:

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma \,}$

Hizkuntza gehienetan, teorema horri kosinuaren teorema deitzen zaio. Frantsesez, ordea, Ghiyath al-Kashi matematikari persiarraren izena du, honek bere aurrekoen emaitzak bateratu baitzituen.

Historia

Euklidesen "Elementuak" K.a. III. mendekoak dira, eta Pitagorasen teoremaren orokortzearen hurbilketa geometrikoa daukate dagoeneko: II. liburuko 12. eta 13. proposizioek bereizita lantzen dituzte triangelu kamuts baten eta triangelu zorrotz baten kasuak. Formulazioa arkaikoa da; izan ere, funtzio trigonometrikorik eta aljebrarik ez zegoenez, azaleren arteko desberdintasunen arabera arrazoitu behar izan zen^[2]. Horregatik, 12. proposamenak termino hauek erabiltzen ditu:

Triangelu kamutsetan, angelu kamutsaren kontrako aldearen karratua handiagoa da triangelua osatzen duten beste bi aldeen karratuen batuketa baino. Diferentzia hori angelu kamutsa angelu zuzen izatera pasatzerakoan gehitu diogun zuzen zatiaren eta luzatu aurretik genuen aldeak osatzen duten laukizuzenaren bikoitza da.

Euclides, Elementuak

ABC triangelua izanik, haren angelu kamutsa C da eta BH, berriz,  B erpinarekiko altuera (ikusi ondoko 2. irudia). Notazio modernoak enuntziatua honela adierazteko aukera ematen du:

${\displaystyle AB^{2}=CA^{2}+CB^{2}+2CACH}$

Erdi Aroko trigonometria arabiar-musulmanari esker, teoremak bere formara eta irismenera eboluzionatzea lortu zen: al-Battani astronomo eta matematikariak Euklidesen emaitza X. mendearen hasieran orokortu zuen, eta horri esker eguzkiaren eta lurraren arteko distantzia angeluarraren kalkuluak egin ahal izan ziren. Garai berean ezarri ziren lehenengo taula trigonometrikoak, sinu eta kosinu funtzioetarako. Horri esker, XV. mendean, Ghiyath al-Kashik^[3], Samarkandako eskolako matematikariak, triangulaziorako modu erabilgarrian jarri zuen teorema. Mendebaldean, François Viètek zabaldu zuen teorema; dirudienez, bere kabuz berraurkitu ondoren^[4].

XVII. mendearen amaieran, notazio aljebraiko modernoak, Eulerrek bere “Introductio in analysin infinitorum” liburuan idatzitako funtzio trigonometrikoen notazio modernoarekin batera, teorema egungo forman idazteko aukera eman zuen, kosinuaren teorema izena zabalduz^[5].

Teorema eta haren aplikazioak

Kosinuaren teorema Pitagorasen teorema orokortua izenaz ere ezaguna da, Pitagorasen teorema kasu berezi bat baita: ${\displaystyle \gamma \,}$ angelua zuzena denean edo, bestela esanda, ${\displaystyle \cos \gamma =0\,}$ denean, kosenoaren teorema honetara murrizten da:

${\displaystyle \,c^{2}=a^{2}+b^{2}}$

eta hori, Pitagorasen teoremaren formulazioa da.

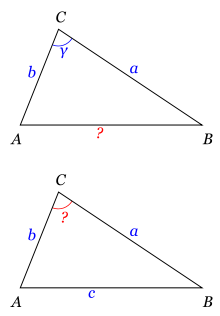
Teorema triangulazioan erabiltzen da (ikusi 3.irudia) triangelu bat ebazteko, eta honako hauek zehazten jakiteko:

• triangelu baten hirugarren aldea, angelu bat eta alboko aldeak ezagutzen ditugunean:

${\displaystyle c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}}$.

• triangelu baten angeluak, hiru aldeak ezagutzen ditugunean:

${\displaystyle \gamma =\arccos {\frac {a^{2}+b^{2}-c^{2}}{2ab}}}$.

Formula horiek aplikatzea zaila da triangelu oso zorrotzak neurtzen direnean metodo sinpleak erabiliz, hau da, c aldea oso txikia denean a eta b aldeekiko ,edo haren baliokidea dena, γ angelua oso txikia denean. Kosinuaren teoremaren korolario bat dago antzekoak diren bi triangeluren kasurako: ABC eta A'B'C'.

${\displaystyle \,cc'=aa'+bb'-(ab'+a'b)\cos \gamma }$.

Frogapenak

Pitagorasen teoremaren arabera

Ikus dezagun kosinuen teorema Pitagorasen teoremaren baliokidea dela ${\displaystyle \gamma }$ angelua zuzena denean. Beraz, c bi angelu zorrotzen ondoan dagoenean kasua eta c angelu zorrotz baten eta kamuts baten ondoan dagoen kasua hartu behar ditugu kontuan.

Lehenengo kasua: c bi angelu zorrotzen ondoan dago.

Har dezagun ondoko irudia. Pitagorasen teoremaren arabera, honela kalkulatzen da c luzera:

(left) ${\displaystyle c^{2}=h^{2}+u^{2}\,}$

Baina h luzera ere horrela kalkulatzen da:

(left) ${\displaystyle h^{2}=a^{2}-(b-u)^{2}\,}$

Bi ekuazioak batuz eta gero sinplifikatuz, hau lortzen dugu:

${\displaystyle c^{2}=a^{2}-b^{2}+2bu\,}$

Kosinuaren definizioaren arabera:

${\displaystyle cos\gamma \,={\frac {b-u}{a}}}$

eta, beraz:

${\displaystyle u=b-a\,\cos \gamma \,}$

u-ren balioa c² rako ekuazioan ordezkatzerakoan hau ondorioztatzen dugu:

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\,\cos \gamma }$

Beraz, lehenengo kasuaren proba amaitu da.

Bigarren kasua: c angelu kamuts baten ondoan dago.

Har dezagun ondoko irudia. Pitagorasen teoremak berriro ezartzen du, ${\displaystyle c^{2}=h^{2}+u^{2}}$ . Baina kasu honetan, ${\displaystyle h^{2}=a^{2}-(b+u)^{2}}$ ekuazioa dugu. Bi ekuazioak konbinatuz, hau lortzen dugu:${\displaystyle c^{2}=u^{2}+a^{2}-b^{2}-2bu-u^{2}}$

${\displaystyle c^{2}=a^{2}-b^{2}-2bu\,}$.

Kosinuaren definiziotik hau dugu ${\displaystyle cos\gamma \,={\frac {b+u}{a}}}$ eta horregatik:

${\displaystyle u=a\,\cos \gamma -b\,}$.

Adierazpenean ordezkatuz, ${\displaystyle c^{2}=a^{2}-b^{2}-2b(a\cos \gamma \ -b)}$ lortzen dugu.

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\,\cos \gamma \,}$.

Hori da frogapenaren amaiera. c² = a² - b² - 2b(a cos(γ) - b) Kontuan hartu behar da, u segmentu bideratutzat hartzen bada, kasu bakarra dagoela, eta bi frogapenak kasu bera bihurtzen direla.

Puntu batek zirkulu batekiko duen potentziagatik

Har dezagun zirkulu bat, zentroa B-n eta BC erradioa dituena, 6. irudian bezala. AC zirkuluaren ukitzailea bada, berriz ere Pitagorasen teorema daukagu. AC ukitzailea ez denean, zirkuluarekin ebakitzen duen beste K puntu bat dago.. A puntuak zirkulu horrekiko duen potentzia hau da:

${\displaystyle AP\cdot AL=AC\cdot AK=AC(AC+CK)}$.

Bestalde, AL = c+a eta AP = c-a da; beraz,

${\displaystyle AP\cdot AL=(c+a)(c-a)=c^{2}-a^{2}}$.

Gainera, CK= -2a cos(g) (ikus eranskina); beraz,

${\displaystyle AC(AC+CK)=b(b-2a\,cos(\gamma ))}$.

Lortutako adierazpenak berdinduz, azkenean hauxe lortzen da :

${\displaystyle c^{2}=a^{2}+b^{2}-2a\;b\,\cos(\gamma )}$

Aurreko frogen aldera, froga honetarako ez da beharrezkoa kasuz kasu azterketa egitea, erlazio aljebraikoak berdinak baitira angelu zorrotzaren kasuan.

Zenbaki konplexuen arabera

Erreparatu eskuineko irudia plano konplexuan.

Hau frogatuko dugu:${\displaystyle |c|^{2}=|a|^{2}+|b|^{2}-2|a|\cdot |b|\cos \gamma }$

Grafikotik,${\displaystyle c=b-a}$.Honen moduluaren karratua kalkulatuz:

${\displaystyle |c|^{2}=|b-a|^{2}}$

Zenbaki konplexuen propietateen arabera, konjokatuen kasuan :(${\displaystyle |u|^{2}=u{\overline {u}}}$)

${\displaystyle |c|^{2}=(b-a){\overline {(b-a)}}}$

${\displaystyle |c|^{2}=(b-a)({\overline {b}}-{\overline {a}})}$

Kontuan izan ${\displaystyle {\overline {a}}=a}$ dela, ${\displaystyle a}$ zenbaki erreala delako (ikus grafikoa).Orduan:

${\displaystyle |c|^{2}=(b-a)({\overline {b}}-a)}$

${\displaystyle |c|^{2}=b{\overline {b}}-a{\overline {b}}-ab+a^{2}}$

${\displaystyle |c|^{2}=b{\overline {b}}-a({\overline {b}}+b)+a^{2}}$

${\displaystyle |c|^{2}=\underbrace {b{\overline {b}}} _{|b|^{2}}-a\underbrace {({\overline {b}}+b)} _{2\Re (b)}+\underbrace {a^{2}} _{|a|^{2}}}$

${\displaystyle |c|^{2}=|b|^{2}-a\cdot 2\Re (b)+|a|^{2}}$

Kontuan izan .${\displaystyle \Re (b)=|b|\cos \gamma }$ (ikus grafikoa) dela. Orduan:

${\displaystyle |c|^{2}=|b|^{2}-a\cdot 2|b|\cos \gamma +|a|^{2}}$

Amaitzeko, kontuan izan ${\displaystyle |a|=a}$ dela (${\displaystyle a}$ zenbaki erreal positiboa delako):

${\displaystyle |c|^{2}=|b|^{2}-|a|\cdot 2|b|\cos \gamma +|a|^{2}}$

${\displaystyle |c|^{2}=|a|^{2}+|b|^{2}-2|a|\cdot |b|\cos \gamma }$ ${\displaystyle \square }$

Kalkulu bektorialarekin

Kalkulu bektoriala erabiliz, are gehiago produktu eskalarra, kosinuaren teorema aurkidaiteke lerro batzuetan:

${\displaystyle c^{2}\,}$	${\displaystyle =\lVert {\overrightarrow {\mathrm {AB} }}\lVert ^{2}}$
	${\displaystyle =\lVert {\overrightarrow {\mathrm {CB} }}-{\overrightarrow {\mathrm {CA} }}\lVert ^{2}}$
	${\displaystyle =\lVert {\overrightarrow {\mathrm {CB} }}\lVert ^{2}-2\cdot {\overrightarrow {\mathrm {CB} }}\cdot {\overrightarrow {\mathrm {CA} }}+\lVert {\overrightarrow {\mathrm {CA} }}\lVert ^{2}}$
	${\displaystyle =\mathrm {CB} ^{2}-2\cdot \left|\mathrm {CB} \right|\cdot \left|\mathrm {CA} \right|\cos {\widehat {\mathrm {ACB} }}+\mathrm {CA} ^{2}}$
	${\displaystyle =a^{2}+b^{2}-2ab\cos \gamma \,}$

Frogapen geometrikoa

ABC triangelua edozein izanik, hau betetzen da:

${\displaystyle AB^{2}=AC^{2}+BC^{2}-2\cdot AC\cdot BC\cdot \cos \gamma .}$

γ angelua 90º bada, proposizioa Pitagorasen teoremara itzultzen da, cos 90º=0 baita. Angelua zorrotza bada, aurreko teorema baten arabera, hau betetzen da:

${\displaystyle AB^{2}=AC^{2}+BC^{2}-2\cdot BC\cdot CD.}$

ACD triangeluan, hau betetzen da:${\displaystyle CD=AC\cos \gamma .}$ Horregatik,

${\displaystyle AB^{2}=AC^{2}+BC^{2}-2\cdot BC\cdot AC\cdot \cos \gamma .}$

Izan bedi, oraingoan, γ angelu kamutsa:

${\displaystyle AB^{2}=AC^{2}+BC^{2}+2\cdot BC\cdot CD,}$

baina ADC triangeluan hau aurkitzen da:^[6]${\displaystyle CD=AC\cdot \cos({\widehat {ACD}}).}$ Hala ere, ACD angelua ABC triangeluaren γ angeluaren betegarria da. Hala, hau lortzen da^[7]: ${\displaystyle \cos({\widehat {ACD}})=-\cos \gamma }$${\displaystyle -AC\cos \gamma }$

Eranskina

Paralelogramo baten azalera

Honela adierazten da:

Paralelogramo baten aldeek a eta b neurtu eta 90°-ko angelua osatuz gero, ab cos(g)-ko azalera izango du.

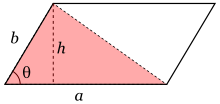
Demagun a eta b aldeak dituen eta θ angelu bat osatzen duen paralelogramo bat, irudian ikusten den bezala. Paralelogramoa diagonal baten bidez zatituz gero, bi eremu triangeluar lortzen dira. Horietako batean, h altuera bat eraikitzen da irudian ageri den moduan.

Eremu triangeluar gorriak ah / 2 azalera du. Definizioz, sin (θ) = h / b, beraz, h = b sin (θ) da. Eremu triangeluarraren  formulan ordezkatzeak honako hau frogatzen du:

Triangelu baten azalera, non aldeek a eta b neurtu eta θ angelua osatzen duten honako hau da: ${\displaystyle A_{T}={\frac {ab\,\sin \theta }{2}}}$

Paralelogramoaren azalera triangeluaren bikoitza dela kontuan hartuta^[8],honako hau ondorioztatzen da.

Paralelogramo baten azalera, non aldeek a eta b neurtu eta θ angelua osatzen duten honako hau da: ${\displaystyle A_{P}=ab\,\sin \theta }$

Ondorioz, ikusten da θ = 90-γ baldin bada, sin (θ) = sin (90 ° -γ) = cos (γ) jarraitzen duela. Hala ere, ikusten da, nahiz eta paralelogramoaren edozein diagonal hartuta ere, froga berdina dela, sin (θ) = sin (180 ° -θ) baita.

Sokak zirkulu batean

Kosinuaren Teoremaren frogapenean, puntu bateko potentzia erabiliz, diagramako CK segmentuak -2a cos (γ) zehazki neurtzen duela adierazten da.

Frogarik errazena CB segmentua luzatzea da zirkunferentzia berriro D puntu batean moztu arte, CD zirkuluaren diametroa izan dadin, zirkuluaren erdigunetik pasatzen baita.

Diametroa izanik, inskribatutako CKD angelua zuzena da nahitaez, beraz, CKD triangelua zuzena da. DCK angeluak θ = 180 ° -γ neurtzen du eta definizioz:

${\displaystyle \cos(\theta )={\frac {CK}{CD}}={\frac {CK}{2a}}}$

eta horregatik,

${\displaystyle CK=2a\cos(\theta )=2a\cos(180^{\circ }-\gamma )=-2a\cos(\gamma )}$

zeren eta cos (180 º - x) = -cos (x) x balioa edozein baita.

Erreferentziak

Ikus, gainera

• Trigonometria
  • Triangelaketa
  • Trigonometria esferikoa
  • Funtzio trigonometrikoa
• Triangeluaren geometria
  • Pitagorasen teorema
  • Sinuaren teorema
• Matematikariak
  • Euclideak
  • Al-Battani
  • Ghiyath al-Kashi
  • François Viète

Bibliografia

• Los Elementos, II. liburukia, Euclides.
• (Ingelesez) Weisstein, Eric W.: "Law of cosines" MathWorld-en.
• Éfimov, N. (1981). Géométrie Supérieure. Moscú: Éditions Mir. OCLC 11732242.
• Lions, Jacques Louis (1980). Petite Encyclopédie des Mathématiques. París: Didier. OCLC 23703843.
• Pogorélov, A. V. (1974). Oinarrizko geometria. Mir argitaletxea, Mosku.'

Kanpo estekak

• Datuak: Q164321
• Multimedia: Law of cosines / Q164321