Algorithmes optimaux de résolution du Rubik's Cube

Les algorithmes optimaux de résolution du Rubik's Cube sont un ensemble d'algorithmes dits optimaux (ou sous-optimaux) permettant de résoudre le casse-tête du Rubik's Cube à partir d'un état quelconque du Cube avec un calculateur.

Il a aussi donné lieu à de nombreuses recherches mathématiques et algorithmiques. On précise les représentations mathématiques du groupe ${\displaystyle G}$ des états du Cube et de ses sous-groupes, nécessaires pour la mise en œuvre effective sur calculateur. Pour l'essentiel, il s'agit des représentations par coordonnées introduites par Kociemba^[1]. Les algorithmes optimaux sont ceux qui peuvent calculer, pour un état arbitraire du Cube, une formule de taille minimale permettant de revenir à l'état résolu .

Rubik's Cube : représentations de base

Notations et abréviations

On oriente le Cube c'est-à-dire on dit quelle face est le Haut, quelle face est l'Avant , ... ainsi nous avons 6 faces dans cet ordre : (H)aut, (B)as, (A)vant, (P)ostérieure, (G)auche, (D)roite

${\displaystyle H,B,A,P,G,D}$

ces lettres désigne alors des rotations de base ou des rotations standards:

H = 90° dans le sens horaire

H' = -90°

H² = 180°.

Remarque : En notation (anglo-saxonne) c' est ${\displaystyle U,D,F,B,L,R}$. .

Les cubes-arêtes sont notés CA et les cubes-sommets CS. Le terme anglais flip est utilisé pour désigner le basculement d'un cube-arête (valeur binaire 0 ou 1), et twist pour désigner la rotation d'un cube-sommet (valeurs 0, 1, 2 (= -1) en tiers de tours dans le sens des aiguilles d'une montre).

Du point de vue mathématique, ${\displaystyle \mathbb {Z} _{n}\equiv \mathbb {Z} /n\mathbb {Z} }$ désigne l'ensemble des entiers modulo n, et ${\displaystyle S_{n}}$ le groupe symétrique des permutations de ${\displaystyle [1..n]}$, dont le cardinal est ${\displaystyle n!}$. La convention est ici de représenter une telle permutation par le vecteur d'entiers images ${\displaystyle p=[p(1),\ldots ,p(n)]}$.

Le groupe M des formules, et le groupe G des états

Le groupe des formules du Cube, engendré par les rotations de base est noté ${\displaystyle M=<H,B,A,P,G,D>}$.

Une formule est donc une suite finie de rotations de base et leur inverse avec la règle suivante:

HH', BB', AA', PP', GG', DD'  ; interdit

par ex:

C = HB'GDA²H' ⇒ ok

K = ABGDD'PH ⇒ interdit à cause DD'

On pose

HH' = BB' = AA' = PP' = GG' = DD' = I

I = formule neutre (ne rien faire, correspond à la permutation identité id)

On définit sur M une loi de composition '.' concaténation :

1) QT , Q suivi de T ; loi interne

2) QI = IQ = Q  ; élément neutre I

3) Q' = Inverse de Q ; on lit à l'envers prime ↔ non-prime par ex:

C' = HA'²D'G'BH'

QQ' = Q'Q = I

4) Q(TV) = (QT)V ; associative

Ainsi (M,.) forme un groupe, le groupe des formules .

Ces formules Q agissent sur l'état du Cube, qui peut se représenter par une permutation ${\displaystyle p_{Q}\in S_{48}}$ des 48 autocollants (stickers) du Cube (les centres ne bougent pas).

Une formule Q engendre donc un état s on va noter :

${\displaystyle e\bullet Q=s}$  ; lire : Q appliqué sur e donne s, ou s provient de Q

e = état résolu,

${\displaystyle s\bullet I=s}$

On considère que 2 formules donnant le même état sont identiques

${\displaystyle e\bullet Q=e\bullet T\Longrightarrow \ Q=T}$

Par ex:

${\displaystyle H'=H^{3}}$

AD'A'D = H'DHD'A'HAH'.

Une visualisation d'un état comme une permutation des autocollants se fait donc par un graphique du type suivant.

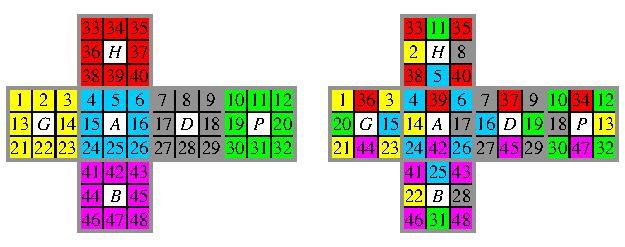
Voici la permutation ${\displaystyle p_{Q}\in S_{48}}$ décrite en cycles disjoints : on reconnait les 12 transpositions (2-cycles)=12 arêtes flipés (arêtes basculés).

p_Q = {2,36},{5,39},{8,37},{11,34},{13,20}, {14,15}, 16,17},{18,19},{22,44},{25,42},{28,45},{31,47}

Ce SuperFlip = q est produit par la formule Q de taille 20f  :

${\displaystyle Q=HD^{2}APDP^{2}DH^{2}GP^{2}DH'B'D^{2}AD'GP^{2}H^{2}A^{2}}$.

${\displaystyle e\bullet Q=q=SuperFlip}$

Le nombre de permutations ${\displaystyle S_{48}}$ est de cardinal ${\displaystyle 48!=1.24139*10^{61}}$, beaucoup plus vaste que le nombre des états possibles.

Décomposition canonique du Cube

On peut caractériser un état du Cube par ces 12 arêtes et leurs orientations et ces 8 sommets et leurs orientations. On montre que tout état du Cube se décompose de façon unique en un quadruplet (permutation des arêtes, orientation des arêtes, permutation des sommets, orientation des sommets) :

${\displaystyle (p,u,r,v)\in S_{12}\times \mathbb {Z} _{2}^{12}\times S_{8}\times \mathbb {Z} _{3}^{8}}$

avec de plus les contraintes suivantes :

• flip total ${\displaystyle \sum _{1}^{12}u_{i}=0\ (mod\ 2)}$,
• twist total ${\displaystyle \sum _{1}^{8}v_{i}=0\ (mod\ 3)}$.
• signatures ${\displaystyle sign(p)=sign(r)}$,

Les permutations sont représentées par les vecteurs des images : ${\displaystyle p=[p(1),\ldots ,p(12)]}$, et de même ${\displaystyle r=[r(1),\ldots ,r(8)]}$.

La définition des orientations des vecteurs u, v dépend d'un choix de marquage sur les facettes du Cube, par ex le marquage ci-contre :

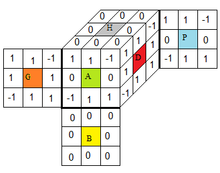
Quel que soit ce choix, on définit la loi de composition de deux états par :

${\displaystyle (p,u,r,v)(p',u',r',v')=(pp',u+p(u'),rr',v+r(v'))}$

avec

${\displaystyle p(u)=(u_{p(1)},u_{p(2)},u_{p(3)},...u_{p(12)})}$

p(u) = permutation des composantes de u

${\displaystyle r(v)=(v_{r(1)},v_{r(2)},v_{r(3)},...v_{r(8)})}$

r(v) = permutation des composantes de v

On en déduit le cardinal du groupe ${\displaystyle \mathrm {card} (G)=12!.2^{12}\times 8!.3^{8}/2.3.2=43252003274489856000\sim 43\times 10^{18}}$.

Pour les démonstrations mathématiques détaillées, on se reportera à la référence^[2], et au livre complet de théorie des groupes^[3], de W.D. Joyner ici [1].

Coordonnées d'un état du cube

Pour effectuer des calculs rapides sur ces états, Kociemba^[1] a introduit une représentation par coordonnées entières, définies ainsi. On associe à une permutation ${\displaystyle p\in S_{n}}$ l'entier ${\displaystyle n_{p}=rang(p)}$, son rang dans l'ordre lexicographique de classement de toutes les permutations. Il faut construire les fonctions calculant le rang, et leurs inverses calculant la permutation associée à un entier donné.

Compte tenu du total nul, le flip ${\displaystyle u=(u_{1},\ldots ,u_{12})}$ est représenté par l'entier ${\displaystyle f_{u}=\sum _{1}^{11}u_{i}2^{i-1}}$, et le twist est représenté par l'entier ${\displaystyle t_{v}=\sum _{1}^{7}v_{i}3^{i-1}}$ (bases 2 et 3). Donc le vecteur de coordonnées du mouvement ${\displaystyle m=(p,u,r,v)}$ est ${\displaystyle coord(m)=(n_{p},f_{u},n_{r},t_{v})}$. Les tailles maximales de ces entiers sont les constantes

${\displaystyle NPCA=12!=479001600,\quad NPCS=8!=40320,\quad NFLIP=2^{11}=2048,\quad NTWIST=3^{7}=2187}$

Rubik's cube : algorithmes optimaux, sous-groupes

La recherche d'algorithmes de reconstruction optimaux (minimum de mouvements) a été entamée par le mathématicien anglais Thistlethwaite en 1981. Il utilise une démarche de décomposition du groupe en quatre sous-groupes ${\displaystyle G\supset G_{1}\supset G_{2}\supset G_{3}\supset G_{4}=\{I\}}$, en se limitant successivement à des carrés (demi-tours) sur les paires de faces opposées ${\displaystyle FP,GD,HB}$.

Par exploration successive des classes à droite de ces sous-groupes ${\displaystyle G_{i+1}\diagdown G_{i}}$, il construit des tables de calcul permettant la résolution complète par une manœuvre de longueur maximale 52f (face-rotation, A² compte 1). Il bornait ainsi le diamètre du groupe de Rubik, c'était le début de la course pour déterminer ce diamètre et obtenir l' Algorithme de Dieu^[4] permettant, pour tout état du cube, de calculer le mouvement minimal de reconstruction. La description de cet algorithme est donnée ici^[5].

L'algorithme à deux phases de Kociemba

Cet algorithme^[1] a été élaboré en 1992. Il utilise la sous-suite de Thistlethwaite ${\displaystyle G\supset G_{2}\supset G_{4}=\{I\}}$,avec le sous-groupe ${\displaystyle G_{2}=<H,B,G^{2},D^{2},A^{2},P^{2}>}$.

Kociemba utilise la caractérisation du groupe intermédiaire ${\displaystyle G_{2}}$ : il n'y a ni flip ni twist, et les CA de la tranche du milieu ${\displaystyle HB}$ y restent, on la notera ${\displaystyle T_{ud}}$. Donc

${\displaystyle e=(p,u,r,v)\in G_{2}\quad \Leftrightarrow \quad u=0,\;v=0,\;p(T_{ud})=T_{ud}}$

La phase 1 consiste à ramener un état quelconque ${\displaystyle g\in G}$, par un mouvement ${\displaystyle x\in G}$, à un état ${\displaystyle g_{2}\in G_{2}}$. On a ${\displaystyle g=g_{2}x^{-1}\in G_{2}x}$, on travaille donc dans l'ensemble des classes à droite (right cosets en anglais) modulo ${\displaystyle G_{2}}$ : ensemble noté ${\displaystyle G_{2}\diagdown G}$.

Une classe est déterminée par un triplet ${\displaystyle (p_{ud},u,v)}$ et les coordonnées associées ${\displaystyle (n_{ud},f_{u},t_{v})}$ avec

• Tranche UD : ${\displaystyle p_{ud}=(1<=i_{1}<i_{2}<i_{3}<i_{4}<=12)}$, images de ${\displaystyle T_{ud}}$. Il y en a 412, la coordonnée est le rang dans la liste ${\displaystyle n_{ud}\in [0..411]}$
• Flip ${\displaystyle u\in \mathbb {Z} _{2}^{11}}$, coordonnée ${\displaystyle f_{u}\in [0..2047]}$,
• Twist ${\displaystyle v\in \mathbb {Z} _{3}^{7}}$, coordonnée ${\displaystyle t_{v}\in [0..2186]}$.

La taille de ${\displaystyle G_{2}\diagdown G}$ est donc ${\displaystyle N_{1}=NFLIP\times NUD\times NTWIST=2217093120\sim 2.2\times 10^{9}}$.

La phase 2 résout le groupe ${\displaystyle G_{2}}$. Un état est représenté par un triplet ${\displaystyle (p_{cs},p_{ud},p_{sl})}$ et les coordonnées associées ${\displaystyle (n_{cs},n_{ud},n_{sl})}$ avec

• Permutation CS : ${\displaystyle p_{cs}\in \mathbb {Z} _{3}^{7}}$, coordonnée ${\displaystyle n_{cs}\in [0..40319]}$
• Permutation CA de ${\displaystyle T_{ud}}$ : ${\displaystyle p_{ud}\in S_{4}}$, coordonnée ${\displaystyle n_{ud}\in [0..23]}$,
• Permutation CA hors ${\displaystyle T_{ud}}$ : ${\displaystyle p_{sl}\in S_{8}}$, coordonnée ${\displaystyle n_{ud}\in [0..40319]}$.

avec la contrainte de Signature totale=1. La taille de G2 est donc ${\displaystyle N_{2}=8!8!4!/2=19508428800\sim 19\times 10^{9}}$.

L'algorithme Cube Explorer^[6] réalise ces deux phases, soit de façon rapide sous-optimale, soit de façon exhaustive optimale et plus lente. Il retourne, pour tout état du cube, une manœuvre de résolution en général de longueur inférieure à 20f. La version initiale de 1992 était sous-optimale et donnait en général des manœuvres de taille inférieure à 23f (mais pas de borne effective prouvée).

L'algorithme optimal (à deux phases) de Reid

La grande étape suivante, vers l'algorithme de Dieu, a été franchie par Michael Reid^[7] en 1997. Il implémente l'algorithme à deux phases de Kociemba, en utilisant une réduction de l'espace de recherche par utilisation de classes d'équivalence (des états ou classes à droite) par les 16 symétries du cube respectant l'axe H-B.

Reid optimal, phase 1

Pour ce faire, il utilise dans la phase 1, une fusion des deux coordonnées ${\displaystyle (permHB=n_{ud},flip=n_{u})}$, en une coordonnée unique ${\displaystyle cl_{fud}\in [0..64429]}$, représentant les classes de symétrie des couples (permHB,flip).

Un élément de ${\displaystyle G_{2}\diagdown G}$ est donc représenté par les coordonnées de symétrie (classe FLIPUD, twist)=${\displaystyle (cl_{fud},t_{v})}$. La taille de l'espace à explorer est donc réduite à

${\displaystyle NSYMG1=NFLIPUD\times NTWIST=140908410}$

avec NUDSLICE=64430 (*---Nombres de classes de symétrie de FLIP-UDslice--*).

Reid optimal, phase 2

Dans cette phase d'exploration complète du groupe G2, on calcule les classes d'équivalence de symétries et inversions des permutations de CS. Il reste 1672 classes. Les classes de symétrie de G2 sont représentées par un triplet de coordonnées ${\displaystyle (cl,u,s)}$ avec

• Classe de permutation des CS : ${\displaystyle \quad cl\in [0..1671]}$
• Permutation des CA hors ${\displaystyle T_{ud}:\quad u\in [0..40319]}$
• Permutation signée des CA de ${\displaystyle T_{ud}:\quad s\in [0..11]}$

La taille de l'espace des classes à explorer est donc :

${\displaystyle NSYMG2=1672\times 40319\times 12=808980480}$

Diamètre du cube et algorithme de Dieu

Puisque le groupe G est fini, il existe pour tout état g une manœuvre de taille minimale (nombre de mouvements élémentaires) qui le ramène à l'état résolu ${\displaystyle e}$. Cette taille minimale est appelée la distance ${\displaystyle d(g,e)}$. Le diamètre du groupe G est ${\displaystyle d(G)=\max(d(g,e),g\in G)}$.

Le diamètre est inférieur ou égal à 29f

Par exploration exhaustive des deux espaces réduits de l'algorithme optimal défini ci-dessus, Mike Reid a établi en 1995^[8] que toutes les classes sont résolues par un mouvement de taille maximale 29f.

Le superflip est à distance 20f !

En recherchant de façon exhaustive des solutions dans l'algorithme optimal à deux phases, Reid démontre le premier, le 18 janvier 1995^[9], que le superflip (l' état où tous les sommets sont bien placés et bien orientés, tous les arêtes sont bien placés mais flipés) est à distance minimale 20f du l'état résolu. Il prouve ainsi que le diamètre du groupe G est supérieur ou égal à 20f. Il n'y a pas de mouvement plus court que celui donné au début de l'article, pour réaliser le superflip.

Le diamètre est 20f

La recherche de l'algorithme de Dieu et du diamètre effectif du groupe G s'est poursuivie de façon continue après 1995, alliant l'augmentation de puissance et taille mémoire des ordinateurs, l'amélioration de l'analyse mathématique du groupe et des algorithmes de recherche. Elle s'est conclue en juillet 2010, par la démonstration du résultat fondamental^[10] :

Le diamètre du groupe de Rubik ${\displaystyle R_{3}}$ est 20f

Ce résultat a été obtenu par un travail conjoint de Tomas Rokicki, Herbert Kociemba, Morley Davidson et John Dethridge. Il a nécessité un temps de calcul de 35 années-CPU, réparti sur un vaste réseau de machines. Il ne donne pas cependant l'algorithme de Dieu, car le programme a cherché pour tous les états (répartis en 2 217 093 120 ensembles de 19 508 428 800 positions chacun) une solution de taille inférieure ou égale à 20f, et non une solution optimale.

Ainsi, le meilleur calcul des mouvements de taille minimale pour résoudre une position est donné par l'algorithme Cube Explorer^[6] , ou l'algorithme de Reid^[11] qui en est une variante antérieure. Ils sont sous-optimaux dans G, car ils utilisent une optimisation séparée en deux phases liées au sous-groupe G2 (mais aussi à ses variantes obtenues par les tranches GD et AP).

Bibliographie

• David Singmaster, Notes on Rubik's magic cube, Enslow Pub Inc, 1981 (ISBN 0-8949-0043-9)
• David Singmaster, Alexander Frey, Handbook of Cubik Math, The Lutterworth Press, 1987 (ISBN 0-7188-2555-1)

Notes et références

Lien externe

• « Fan2Cube », sur fan2cube.fr (consulté le 14 décembre 2023)

• Portail des jeux
• Portail de l'informatique théorique