Processus de Galton-Watson
Le processus de Galton-Watson (ou processus de Bienaymé-Galton-Watson) est un processus stochastique permettant de décrire des dynamiques de populations. C'est un cas particulier de processus de branchements.
Historique

À l'origine, ce modèle a été introduit par Bienaymé en 1845 et indépendamment par Galton en 1873 en vue d'étudier la disparition des patronymes[1].
Supposons que chaque adulte mâle transmette son patronyme à chacun de ses enfants. Supposons également que le nombre d'enfants de chaque homme soit une variable aléatoire entière (et que la distribution de probabilité soit la même pour tous les hommes dans une lignée). Alors, un patronyme dont les porteurs ont un nombre d'enfant strictement inférieur à 1 en moyenne est amené à disparaître. Inversement, si le nombre moyen d'enfants est supérieur à 1, alors la probabilité de survie de ce nom est non nulle et en cas de survie, le nombre de porteurs du patronyme connaît une croissance exponentielle.
Formulation générale
On suppose l'existence d'une population d'individus qui se reproduisent de manière indépendante. Chaque individu i donne naissance à individus et meurt. On suppose que les sont des variables aléatoires indépendantes à valeurs entières suivant la distribution Par exemple,
- si, avec probabilité alors l'individu i meurt sans se reproduire ;
- si, avec probabilité alors il y a un remplacement un-pour-un de l'individu i ;
- etc.
Notation — La fonction génératrice associée à la distribution de probabilité définie par :
est d'une importance particulière dans la discussion des résultats essentiels sur les processus de Galton-Watson.
Paramètre critique et classification des processus de Galton-Watson
Notons la taille de la population à la n-ème génération. On suppose souvent que la population possède un seul ancêtre, ce qui se traduit par
Le nombre
désigne le nombre moyen d'enfants d'un individu typique de la population considérée. L'évolution de la taille moyenne de la population est gouvernée par la formule de récurrence suivante, conséquence de la formule de Wald :
d'où il résulte que
Définition — Si, à partir d'un certain rang, tous les termes de la suite sont nuls, on dit qu'il y a extinction de la population.
Classification des processus de Galton-Watson — Il existe deux régimes séparés par une valeur critique du paramètre :
- Si m < 1, le processus de Galton-Watson est dit sous-critique. L'extinction de la population se produit avec probabilité 1 ;
- Si m > 1, le processus de Galton-Watson est dit sur-critique. Alors la probabilité de survie de ce nom est non nulle (la probabilité d'extinction est inférieure strictement à 1). En cas de survie, le nombre de porteurs du patronyme connaît une croissance exponentielle.
- Si m = 1, alors le processus de Galton-Watson est dit critique. Son comportement est plus complexe et sera discuté dans la suite.
Notation de Neveu
La notation de Neveu[2] permet de décrire rigoureusement l'évolution de la population à l'aide d'un arbre planaire enraciné, qui est en fait l'arbre généalogique de cette population. Cet arbre planaire enraciné peut être décrit de manière non ambigüe par la liste de ses sommets, chacun désigné par une suite finie d'entiers, qui sont les positions, au sein de leur fratrie, des ancêtres (ou ascendants) de ce sommet : le sommet 2|4|3 désigne le 3e fils du 4e fils du 2e fils de l'ancêtre (l'ancêtre étant lui-même désigné par la suite vide, notée ). Par convention, l'ancêtre est le sommet initial de l'arête racine, et le sommet final de l'arête racine est le fils ainé de l'ancêtre : en tant que tel, il est donc noté 1. La longueur de la suite associée à un sommet est la hauteur (ou la profondeur) du sommet, i.e. la distance entre ce sommet et le début de la racine, qui représente l'ancêtre : en filant la métaphore, un sommet de hauteur n représente un individu appartenant à la n-ème génération de la population fondée par l'ancêtre. Les 5 arbres à 3 arêtes :
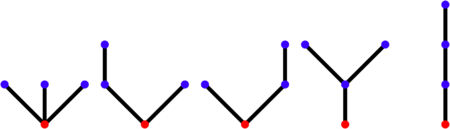
sont ainsi décrits par les 5 ensembles de mots
Avec cette notation, un arbre planaire encode commodément une réalisation de processus de Galton-Watson avec extinction : cet arbre est alors appelé arbre de Galton-Watson. Rien ne s'oppose à définir un arbre planaire infini à l'aide de la notation de Neveu, ce qui permet d'encoder les réalisations de processus de Galton-Watson où la population ne s'éteint pas.

L'arbre de la figure ci-contre correspond à une suite de variables aléatoires ainsi définies :
Ainsi, un processus de Galton-Watson peut-être vu comme une fonctionnelle déterministe d'une famille de variables aléatoires indépendantes et de même loi la variable désignant la progéniture de l'individu i (le nombre d'enfants auxquels il donne naissance en mourant). Ici désigne l'ensemble (dénombrable) des suites d'entiers de longueurs finies (éventuellement de longueur nulle dans le cas de ) :
Certaines variables aléatoires de la suite n'ont pas d'influence sur le processus de Galton-Watson : dans l'exemple ci-contre, ou n'ont pas d'importance car l'ancêtre a strictement moins de 4 enfants () et l'individu 12 a strictement moins de 6 enfants (). De même les progénitures des individus de la 5e génération (les correspondant aux suites i de longueur 5) n'influencent pas cette réalisation du processus de Galton-Watson, car la population s'éteint à la 4e génération ().
Étude fine de la taille des générations
Notons la fonction génératrice de la variable aléatoire définie par
Posons
où les Xi sont des variables aléatoires indépendantes, toutes de loi ; est la k ème puissance de convolution de la loi
En vertu de la propriété de composition des fonctions génératrices, on a la relation suivante :
Pour pouvoir appliquer la propriété de composition des fonctions génératrices, il faut se convaincre que (l'effectif de la n+1 ème génération) a même loi que la somme de variables aléatoires indépendantes, toutes de loi et indépendantes de Bien sûr, est la somme des progénitures des individus appartenant à la n ème génération, mais, contrairement au contexte de la propriété de composition des fonctions génératrices, on ne choisit pas les premiers termes d'une suite de variables aléatoires i.i.d. indexées par : dans la notation de Neveu, par exemple, la suite de variables aléatoires i.i.d. est indexée par et les variables de la suite intervenant dans la somme sont choisies en fonction de toute l'histoire de la population, jusqu'à la n-ème génération (non incluse). Une fois qu'on s'est convaincu que, malgré cela, (l'effectif de la n+1 ème génération) a même loi que la somme de variables aléatoires indépendantes, toutes de loi et indépendantes de on en déduit que
Un énoncé précis utilise la notion de loi conditionnelle : pour pouvoir appliquer la propriété de composition des fonctions génératrices, on doit vérifier que, pour tout k, la loi conditionnelle de sachant l'évènement est la loi de la somme de k variables aléatoires indépendantes, toutes de loi loi décrite par Pour vérifier cela, on est amené à calculer la loi conditionnelle sachant un évènement plus précis que i.e. sachant la composition exacte de la n-ème génération. Soit L un ensemble d'éléments de Notons l'évènement :
En particulier les ancêtres des individus appartenant à L sont connus, donc apporte une information sur les générations 1, 2, ... jusqu'à la génération n-1. On constate que l'évènement appartient à la tribu engendrée par la famille des où i est une suite de longueur inférieure ou égale à n-1. Par ailleurs,
Comme L est disjoint de l'ensemble des suites de longueur inférieure ou égale à n-1, le lemme de regroupement entraîne que
Cette dernière probabilité dépend de mais, surtout, elle dépend de L uniquement à travers son cardinal Donc, dès que
en vertu d'une variante de la formule des probabilités totales. Accessoirement ceci montre que la suite possède la propriété de Markov. Plus précisément, c'est une chaine de Markov homogène de probabilité de transition
En remarquant que
on en déduit, par récurrence, que
puis la relation de récurrence fondamentale. On peut aussi obtenir cette relation plus directement, en décomposant différemment (comme somme de X copies de plutôt que comme somme de copies de X).
- La relation de récurrence sur l'espérance de
- découle alors de la formule de dérivation des fonctions composées.
- À l'aide de la relation de récurrence fondamentale, on trouve aussi, le cas échéant, une formule de récurrence pour la variance de
- La démonstration de la formule de récurrence fondamentale montre aussi (modulo quelques modifications) que la suite est une chaine de Markov dont la matrice de transition est définie par
Cas sur-critique
Dans le cas sur-critique, la taille de la population croît à vitesse exponentielle sur un ensemble assez large.
Théorème — Si la loi de la progéniture est intégrable, de moyenne m>1, alors il existe une variable aléatoire M telle que, presque sûrement,
Si, de plus, la loi de la progéniture est de carré intégrable, alors Par ailleurs, converge vers M dans L2.
Des résultats plus précis peuvent être obtenus grâce au théorème de Kesten-Stigum[3],[4].
Soit une famille indépendante et identiquement distribuée de variables aléatoires de loi , de moyenne . On définit la filtration :
Alors le processus défini par récurrence par :
est un processus de Galton-Watson de loi de reproduction . On définit alors le processus :
qui est une -martingale. En effet,
ce qui entraîne que
Comme est une martingale positive, elle converge presque sûrement vers une variable aléatoire réelle
Si on suppose de plus que , on peut démontrer que l'ensemble est de mesure positive, et qu'il est égal presque sûrement à l'ensemble de non-extinction de l'arbre En effet, dans ce cas, un calcul par récurrence montre que est bornée dans On en déduit alors la convergence dans de vers . On a alors, en particulier,
Par conséquent sur un ensemble de mesure non nulle.
Ainsi, presque sûrement, est une bonne approximation, au premier ordre, du nombre d'individus de la génération du moins sur l'ensemble ensemble qui a une probabilité non nulle.
Un calcul explicite
Il y a assez peu d'exemples où la formule de récurrence fondamentale conduit à un calcul explicite de L'exemple le plus connu est celui où la loi de reproduction est un mélange de masse de Dirac en 0 et de loi géométrique,
d'espérance
Cela correspond exactement aux fonctions génératrices qui sont des homographies :
D'après la classification des homographies en fonction du nombre de points fixes, l'homographie est conjuguée à des applications dont les itérées se calculent simplement, à savoir à dans les cas non critiques (deux points fixes, 1 et ) et à dans le cas critique (un point fixe double, 1).
Cas non critique
Dès que on trouve, par diagonalisation d'une application linéaire associée à l'homographie
ce qui entraine
et conduit à un calcul explicite de
Cas critique
Le cas est le cas critique On trouve, toujours en raisonnant sur une application linéaire (non diagonalisable) associée à l'homographie
donc
Finalement est une homographie :
ce qui correspond au choix de paramètres suivant :
Ici T désigne la date d'extinction, i.e. le numéro de la première génération vide.
Probabilité d'extinction
Théorème — La probabilité d'extinction d'un processus de Galton-Watson dont la distribution de la progéniture est est la plus petite solution, dans l'intervalle [0,1], de l'équation :
Cela résulte de ce que
d'où il suit, par propriété de limite croissante, que
Par ailleurs la suite
est définie par (car ), et par la relation de récurrence
ce qui conduit à voir comme un point fixe de φ.
Pour démontrer la relation de récurrence sur notons que
Donc
Maintenant, supposons qu'il existe un point fixe de dans l'intervalle [0;1]. Alors, la fonction étant croissante sur l'intervalle [0;1], entraine puis, par récurrence, Mais, d'une part, (ce qui peut être réécrit ), d'autre part Ainsi, la suite est croissante et majorée par 1, donc convergente. De plus, on a vu que la suite est majorée par tout point fixe de appartenant à l'intervalle [0;1]. La limite de la suite est donc, elle aussi, majorée par tout point fixe de appartenant à l'intervalle [0;1]. Mais comme la fonction est continue sur l'intervalle [0;1], sa limite est un des points fixes de la fonction donc, forcément, le plus petit d'entre eux.
Comme est une série entière de rayon de convergence au moins égal à 1, à coefficients positifs ou nuls, est convexe (et même strictement convexe si p0+p1<1), et indéfiniment dérivable sur l'intervalle ]0,1[, et possède donc au plus 2 points fixes dans l'intervalle [0;1], sauf si Un théorème analogue concernant les cartes planaires aléatoires (une généralisation naturelle des arbres aléatoires) a été démontré en 2007[5].

- si le théorème dit que la probabilité d'extinction est nulle. Cela peut être vu directement sans difficulté, car équivaut à ce qui entraine immédiatement que chaque génération est constituée d'exactement un individu ;
- plus généralement, si 0 est point fixe, donc, d'après le théorème, est nulle (on pouvait le voir directement, puisque, en ce cas, chaque individu de la population a au moins un enfant) ;
- si les deux points fixes sont 1 et donc, comme on pouvait s'y attendre, la probabilité d'extinction vaut 1 si et vaut moins que 1 (en fait ) si Ici, la valeur de est difficile à calculer directement, sans utiliser le théorème. La figure ci-contre montre plusieurs valeurs de et la probabilité d'extinction correspondante.
Plus généralement
Théorème — On distingue 3 cas :
- Cas souscritique (m<1). La probabilité d'extinction vaut 1.
- Cas critique (m =1). La probabilité d'extinction vaut 1, sauf si et, dans ce dernier cas, la probabilité d'extinction est nulle.
- Cas surcritique (m>1). La probabilité d'extinction est strictement inférieure à 1 (et est le plus petit point fixe de φ dans l'intervalle [0;1]).
Cela résulte de ce que
En effet :
- Cas sous-critique. Si m<1, la tangente en (1;1) au graphe de φ est, dans l'intervalle [0;1[, strictement au-dessus de la droite d'équation y=x, et, φ étant convexe, le graphe de φ est au-dessus de sa tangente, donc, lui aussi, strictement au-dessus de la droite d'équation y=x : le seul point fixe de φ est 1.
- Cas critique. Si m =1, la tangente en (1;1) au graphe de φ est la droite d'équation y=x. Si φ est strictement convexe, le graphe de φ est strictement au-dessus de sa tangente, donc le seul point fixe de φ est 1. Or φ est strictement convexe si et seulement si (comme on le voit en calculant la dérivée seconde de φ). Sinon φ est une fonction affine, donc son graphe est confondu avec ses tangentes, en particulier, ici, avec la droite d'équation y=x. Donc
- Cas surcritique. Si m>1, la tangente en (1;1) au graphe de φ est strictement au-dessous de la droite d'équation y=x, donc, sur un intervalle [1-ε,1[ bien choisi, φ lui-même est strictement au-dessous de la droite d'équation y=x. En 0, par contre, comme le graphe de φ est au-dessus de la droite d'équation y=x. Donc, en vertu du théorème des valeurs intermédiaires, φ possède un point fixe strictement plus petit que 1.
Le comportement du processus de Galton-Watson dans les cas sous-critique et surcritique correspond à l'intuition. Par contre, le comportement du processus de Galton-Watson dans le cas critique aléatoire (l'extinction est certaine) est radicalement différent du comportement du processus de Galton-Watson dans le cas critique déterministe (chaque individu a exactement un enfant et l'extinction est impossible).
À voir aussi
Notes
- ↑ « Three papers on the history of branching processes », sur stat.washington.edu (consulté le )
- ↑ Jacques Neveu, « Arbres et processus de Galton-Watson », Ann. de l'IHP, vol. 22, no 2, (lire en ligne) (section 2)
- ↑ (en) H. Kesten et B. P. Stigum, « A Limit Theorem for Multidimensional Galton-Watson Processes », The Annals of Mathematical Statistics, vol. 37, no 5, , p. 1211-1223 (lire en ligne)
- ↑ (en) Krishna B. Athreya, « A Simple Proof of a Result of Kesten and Stigum on Supercritical Multitype Galton-Watson Branching Process », The Annals of Mathematical Statistics, vol. 41, no 1, , p. 195-202 (lire en ligne)
- ↑ (en) Jean-François Marckert et Grégory Miermont, « Invariance principles for random bipartite planar maps », Ann. Probab., vol. 35, no 5, , p. 1642-1705 (DOI 10.1214/009117906000000908, lire en ligne), Proposition 1.
Bibliographie
- (en) Krishna B. Athreya et Peter E. Ney, Branching processes, Dover Publications, , 2e éd., 304 p. (ISBN 978-0-486-43474-2, lire en ligne)
- (en) Theodore E. Harris, The theory of branching processes, Dover Publications, , 2e éd., 256 p. (ISBN 978-0-486-49508-8)
- L'article original de Galton et Watson: On the Probability of the Extinction of Families
Liens utiles
- Francis Galton
- Henry William Watson
- Arbre (graphe)
- Arbre de Galton-Watson
- Formule de Wald
- Fonction génératrice
- Chaîne de Markov
- Propriété de Markov
 Portail des probabilités et de la statistique
Portail des probabilités et de la statistique








![{\displaystyle \varphi (s)\ =\ \sum _{n\geq 0}\,p_{n}\,s^{n}\ =\ \mathbb {E} \left[s^{X_{i}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c867ce73c49aaf772099af80d03736fd9cbdb7c)



![{\displaystyle \mathbb {E} [Z_{n+1}]\ =\ m\ \mathbb {E} [Z_{n}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6acb303289ae53c67c58eed9ece6d746fe952a8)
![{\displaystyle \mathbb {E} [Z_{n}]\ =\ m^{n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e418ae0fede82193c7c38285550335c496da48a3)
















![{\displaystyle \varphi _{n}(s)\ =\ \sum _{k\geq 0}\,\mathbb {P} (Z_{n}=k)\,s^{k}\ =\ \mathbb {E} \left[s^{Z_{n}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b5c33b08473366c396d55d146c416e5805871b3)
![{\displaystyle p_{\ell }^{\star k}\ =\ [s^{\ell }]\varphi ^{k}(s)\ =\ \mathbb {P} (X_{1}+\dots +X_{k}=\ell ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c3f7cfe931711088327395ce89f36c8c4fc3ad7)

























![{\displaystyle \mathbb {E} [Z_{n+1}]\ =\ \varphi ^{\prime }\left(1\right)\ \mathbb {E} [Z_{n}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3466ed0f1233b19336539d45fe772326b01c9b43)













![{\displaystyle {\begin{aligned}\mathbb {E} \left[Z_{n+1}\left|{\mathcal {F}}_{n}\right.\right]&=\mathbb {E} \left[\sum _{i=1}^{Z_{n}}X_{i,n+1}\left|{\mathcal {F}}_{n}\right.\right]\\&=\sum _{i=1}^{Z_{n}}\mathbb {E} \left[X_{i,n+1}\left|{\mathcal {F}}_{n}\right.\right]\\&=mZ_{n},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eab051f0e7e08206d54952812274d414208ca31d)
![{\displaystyle \mathbb {E} \left[M_{n+1}\left|{\mathcal {F}}_{n}\right.\right]=M_{n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864a9d4a5a20b2cf3b9afcc17ef004577cb1cabf)


![{\displaystyle \mathbb {E} [X_{i,j}^{2}]\ <\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a4b7fba6a360741e369ae1b5eefd8eb1ca6a382)





![{\displaystyle \mathbb {E} [M]=\lim _{n}\mathbb {E} [M_{n}]=\mathbb {E} [M_{0}]=\mathbb {E} [Z_{0}]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61752854931da640130160564f9a510980096f88)






![{\displaystyle \mathbb {P} (X_{i}=k)\ =\ \alpha 1\!\!1_{k=0}+(1-\alpha )(1-p)^{k-1}p\,1\!\!1_{k\geq 1},\quad (\alpha ,p)\in [0,1]\times ]0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d4e547265c288af0ee6a4fef25527efa1c4f988)
![{\displaystyle m\ =\ \mathbb {E} [X_{i}]\ =\ {\frac {1-\alpha }{p}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9ec8650082bbfd97651ea0c80c0eb0ffbb6c795)




























































