Fogyasztáselmélet (mikroökonómia)

A fogyasztáselmélet a mikroökonómia egyik legfontosabb területe a termeléselmélet mellett. Azt vizsgálja, hogy a racionális egyének, illetve háztartások adott jövedelem és árak mellett milyen javakat fogyasztanak, hogyan osztják meg a fogyasztásukat jelen és jövő között, továbbá mennyi időt töltenek munkával és mennyit szabadidővel.

A fogyasztási döntés

Ahhoz, hogy az egyének, illetve háztartások fogyasztási döntéseit vizsgálhassa, a döntést befolyásoló tényezőket a fogyasztáselmélet két csoportba sorolja.

• Az első csoportba azok a külső környezet által meghatározott tényezők tartoznak, amelyekről – itt – feltételezzük, hogy az egyén nem képes befolyásolni őket: a két legfontosabb a jövedelem és a javak ára; de ide tartoznak még az esetleges adók, támogatások, mennyiségi korlátozások is. Ezek a tényezők korlátot emelnek az egyén döntése elé.
• A másik csoportot az egyén preferenciarendszere alkotja: ez a belső tényező, amely meghatározza, hogy két jószágkombináció (jószágkosár) közül az egyiket preferálja-e, azaz szívesebben fogyasztja, vagy pedig a két jószágkombináció egymással közömbös.

Hogy az egyén számára melyik(ek) a legjobb, az optimális jószágkombináció(k), a két tényezőcsoport együttesen fogja meghatározni. Egész pontosan az a jószágkombináció lesz optimális, amely a külső tényezők korlátjai mellett az egyén számára elérhetők közül a leginkább preferált. Egyszerűbben: az elérhetők közül a legjobb.

Mivel pedig a mikroökonómia feltételezi, hogy az egyének (és a háztartások) racionális döntéshozók, megállapíthatjuk: a ténylegesen választott jószágkombináció egybe fog esni az optimálissal.

A fogyasztási döntés kétjószágos modellje

Ahhoz, hogy a döntést befolyásoló tényezőket, illetve a magát a döntést matematikai eszközökkel modellezni tudjuk, több egyszerűsítést is be kell vezetnünk. A legegyszerűbb modellben feltételezzük, hogy csak két jószág van, amivel kapcsolatban döntést kell hoznunk. Ebben az esetben a jószágkombinációkat ábrázolhatjuk egy derékszögű koordináta-rendszerben, amelynek egyik tengelye az 1. jószág, másik tengelye a 2. jószág mennyiségét reprezentálja. Ezt a koordináta-rendszert – pontosabban annak első síknegyedét, hiszen mindkét jószágot csak nemnegatív mennyiségben tudjuk értelmezni – jószágtérnek is nevezzük. A jószágtér minden pontja egy-egy jószágkombinációval egyenértékű.

Külső tényezők: a költségvetési korlát

A jövedelem és az árak

A legegyszerűbb esetben, ha külső tényezőként csak a pénzben kifejezett jövedelem (m), illetve a két jószág ára (p₁ és p₂) jelenik meg, az egyén számára elérhető, vagyis megfizethető (x₁, x₂) jószágkombinációk halmazára a következő egyenlőtlenség teljesül:

${\displaystyle p_{1}x_{1}+p_{2}x_{2}\leq m}$

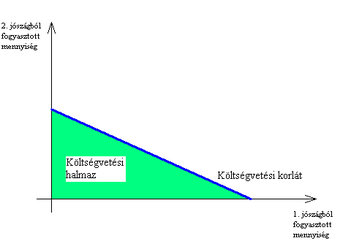
Ezt az egyenlőtlenséget nevezzük a fogyasztó költségvetési korlátjának. Azon ${\displaystyle x_{1}}$, és ${\displaystyle x_{2}}$ kombinációk halmazát, melyek teljesítik ezt az egyenletet, a fogyasztó költségvetési halmazának nevezzük. A költségvetési halmaz ebben az esetben háromszög alakú, és a két tengely, valamint az úgynevezett költségvetési egyenes határolja. Ez azokat a jószágkombinációkat tartalmazza, amelyek még éppen elérhetők, vagyis az egyén a teljes jövedelmét felhasználja a megvásárlásukra.

A költségvetési egyenes egyenlete tehát:

${\displaystyle p_{1}x_{1}+p_{2}x_{2}=m\,}$

Ezt átrendezve:

${\displaystyle x_{2}={\frac {m}{p_{2}}}-{\frac {p_{1}}{p_{2}}}x_{1}}$

Amiből látszik, hogy a függvénygörbe (költségvetési egyenes) az ${\displaystyle x_{2}}$ tengelyt az ${\displaystyle {\frac {m}{p_{2}}}}$ pontban, az ${\displaystyle x_{1}}$ tengelyt az ${\displaystyle {\frac {m}{p_{1}}}}$ pontban metszi, meredeksége pedig ${\displaystyle -{\frac {p_{1}}{p_{2}}}}$. Utóbbinak az optimum megválasztásakor lesz jelentősége.

Ha legalább az egyik jószágból érdemes minél többet fogyasztani, logikusnak tűnik az az állítás, hogy a racionális egyén minden jövedelmét elkölti, azaz a költségvetési korláton lévő jószágkombinációk közül választ. Ezt úgy is szokás mondani, hogy az egyén fogyasztására teljesül Walras törvénye. Ha viszont mindkét jószág káros jószág, akkor a fogyasztó még mindig jobban jár, ha marad elköltetlen jövedelme, mint hogyha számára „negatív hasznossággal” járó jószágkombinációt vásárolna. Így Walras törvénye nem teljesül ebben az esetben. A továbbiakban viszont mindkét jószágról feltételezzük, hogy hasznosak.

A költségvetési korlát jövedelemnövekedés hatására „kijjebb” tolódik, hiszen mind az ${\displaystyle m/p_{2}}$, mind az ${\displaystyle m/p_{1}}$ zérushelyek értéke megnő, ráadásul azonos mértékben. Jövedelemcsökkenés következtében a költségvetési korlát „beljebb” tolódik (zérushelyek értéke csökken). Meredeksége azonban nem változik, hiszen a ${\displaystyle -p_{1}/p_{2}}$ tört értéke független a jövedelemtől, csak az áraktól függ. Ennek megfelelően a költségvetési halmaz nagyobb, illetve kisebb lesz.

Árváltozás esetén, tehát ha ${\displaystyle p_{1}}$ vagy ${\displaystyle p_{2}}$ értéke változik, akkor a költségvetési korlát egyik tengelymetszete (${\displaystyle m/p_{2}}$, ill. ${\displaystyle m/p_{1}}$) változatlan marad, meredeksége viszont megváltozik. Abban az esetben, ha csak az egyik ár változik meg, akkor az árnövekedés mindig csökkenti, míg az árcsökkenés növeli a költségvetési halmaz területét.

Adók

A kivethető adókat a fogyasztáselmélet három csoportba sorolja.

• Ha egy jószágot mennyiségi adó terhel, akkor a jószág minden egységének vásárlásakor egy meghatározott összeget kell adóként kifizetni. Speciális esetben ez az összeg változhat is a mennyiség függvényében, például előfordulhat, hogy bizonyos mennyiségig nem kell adót fizetni. Az 1. jószágra kivetett, egységesen t összegű mennyiségi adó hatására a költségvetési korlát egyenlete ilyen alakot ölt:

${\displaystyle (p_{1}+t)\cdot x_{1}+p_{2}x_{2}=m\,}$

Úgy is mondhatjuk tehát, hogy a mennyiségi adó hatása ugyanolyan, mintha a jószág ára t pénzegységgel növekedne.

• Az értékadó vagy ad valorem adó fogyasztáselméleti hatását tekintve megfeleltethető a mennyiségi adónak, csak itt a „pluszban” kifizetendő összeg a jószág árának százalékában van megadva. Ezt a százalékos arányt τ-val (tau) jelöljük. A módosult költségvetési korlát:

${\displaystyle (1+\tau )\cdot p_{1}\cdot x_{1}+p_{2}x_{2}=m\,}$

• Az egyösszegű adó egy olyan konstans érték, amit mindenképpen meg kell fizetni, függetlenül attól, hogy a jószágból mekkora mennyiséget fogyasztunk. Ezért az egyösszegű adó (T) a jövedelmünket csökkenti. Matematikai formában:

${\displaystyle p_{1}x_{1}+p_{2}x_{2}=m-T\,}$

Támogatások

A támogatások mindegyike megfeleltethető az adófajtáknak, csak hatásuk azokéval ellentétes. A mennyiségi és az értékbeli támogatás (ismertebb nevén ártámogatás) a költségvetési korlát meredekségét változtatja meg – az árcsökkenéssel azonos módon –, míg az egyösszegű támogatás a felhasználható jövedelem növekedését eredményezi.

Mennyiségi korlátozások

Ilyesmik több okból is előfordulhatnak:

• Az adott jószágból nagyon kevés áll rendelkezésre, olyannyira, hogy ha az összeset megvásároljuk, még akkor is marad jövedelmünk. Bizonyos luxuscikkek esetén gyakran előfordul ez az eset.
• A hatóságok adminisztratív eszközökkel megakadályozzák, hogy az adott jószágból egy egyén vagy háztartás a megengedettnél többet vásároljon. A jegyrendszer, amit főként háborúk idején alkalmaznak, tipikus példa erre a fajta korlátozásra.

A mennyiségi korlátozás hatására a költségvetési korlát „megtörik”, a költségvetési halmaz pedig elveszti hagyományos háromszög alakját.

Fontos megjegyezni, hogy az imént tárgyalt három külső tényező – adó, támogatás és mennyiségi korlátozás – természetesen megjelenhet együttesen is. (Elképzelhető mondjuk olyan jószág, amelyre bizonyos mennyiségig támogatás jár, azután adó terheli, egy meghatározott mennyiségen túl pedig már nem is szabad belőle vásárolni.)

Belső tényezők: a preferenciák

Nem beszéltünk még a fogyasztási döntéshez szükséges belső tényezők matematikai modelljéről. A preferenciákra vonatkozó bizonyos feltételeket elfogadva megállapíthatjuk, hogy bármely két jószágkombinációt kiválasztva, megmondható, hogy azok közömbösek-e egymáshoz képest, vagy ha nem, melyik jobb a kettő közül. Kézenfekvőnek tűnik, hogy a preferenciák matematikai modellezésekor ezekhez a jószágkombinációkhoz számokat rendeljünk.

Definiáljuk az ${\displaystyle U(x_{1},x_{2})\,}$ kétváltozós függvényt, amely minden (x₁, x₂) jószágkombinációhoz egy számértéket rendel úgy, hogy ha az egyik jószágkosár legalább olyan jó, mint a másik, akkor a hozzá tartozó U érték is legyen nagyobb vagy azonos. ${\displaystyle U(x_{1},x_{2})\,}$ tehát egy kétváltozós hasznossági függvény.

Nyilvánvaló, hogy ha kiválasztunk két konkrét U értéket, U₁-et és U₂-t, csak az a fontos számunkra, hogy egyenlőek-e, illetve melyik a nagyobb, az nem, hogy pontosan mennyivel. Így ha az ${\displaystyle U(x_{1},x_{2})\,}$ függvény valamilyen preferenciarendezést ír le, akkor mondjuk a ${\displaystyle 2\cdot U(x_{1},x_{2})}$ függvény is alkalmas ugyanennek a fogyasztói ízlésvilágnak a modellezésére. Általánosságban: ha f szigorúan monoton növekvő függvény, akkor ${\displaystyle f(U)\,}$ U-val azonos preferenciákat reprezentál. Ilyen monoton transzformációk például: konstans hozzáadása, pozitív konstanssal való szorzás, hatványozás, stb.

Egyértelmű, hogy az U-t, mint kétváltozós függvényt, nem tudjuk ábrázolni a jószágtérben. Néhány különböző U értékhez tartozó szintvonalát viszont megrajzolhatjuk. Ezeket a szintvonalakat közömbösségi görbéknek hívjuk, mert a rajtuk lévő jószágkombinációkhoz tartozó U érték azonos, vagyis egymáshoz képest ezek a jószágkosarak közömbösek.

A közömbösségi görbék meredekségét helyettesítési határaránynak nevezzük. (Jelölése az angol "marginal rate of substitution"-ből MRS.) Ez az arány – kicsit pontatlanul fogalmazva – azt mutatja meg, hogy mennyivel kell hogy változtassunk az 1. jószágból fogyasztott mennyiségen, ha a 2. jószágból eggyel többet kívánunk fogyasztani, de nem akarjuk, hogy változzon a hasznossági függvényünk értéke. Negatív meredekségű közömbösségi görbék esetén a helyettesítési határarány is negatív, azaz csak úgy tudunk valamelyik jószágból többet vásárolni, ha a másik jószágból lemondunk valamekkora mennyiségről.

Ha az ${\displaystyle U(x_{1},x_{2})\,}$ függvény x₁ szerinti parciális deriváltját (az 1. jószág határhasznát) ${\displaystyle MU_{1}\,}$-gyel, x₂ szerinti parciális deriváltját (a 2. jószág határhasznát) pedig ${\displaystyle MU_{2}\,}$-vel jelöljük, a helyettesítési határarányra – a differenciálszámítás szabályai szerint – az alábbi összefüggésnek kell teljesülnie:

MRS${\displaystyle =-{\frac {MU_{1}}{MU_{2}}}}$

Optimum

Optimális jószágkombinációnk a költségvetési halmaz azon pontjában vagy pontjaiban lesz, ahol a hasznossági függvény értéke, vagyis az U érték maximális. Sok speciális eset fordul elő, de – mint már említettük – többnyire ez a pont a költségvetési korláton található, és annak belső pontja. Ekkor pedig ez a pont az lesz, ahol a közömbösségi görbék egyike éppen érinti a költségvetési korlátot. Ugyanis ha metszéspontban volnánk, a költségvetési korláton „befelé” elmozdulva még magasabb U értékhez tartozó jószágkombinációkat találnánk.

Az érintési pontban viszont a helyettesítési határarány (a közömbösségi görbe meredeksége) egyenlő a költségvetési korlát meredekségével:

MRS${\displaystyle =-{\frac {p_{1}}{p_{2}}}}$

Amiből:

${\displaystyle {\frac {MU_{1}}{MU_{2}}}={\frac {p_{1}}{p_{2}}}}$

Az eredmény nemcsak matematikai, hanem közgazdasági szempontból is érthető. Nyilvánvalónak tűnik, hogy ott találunk optimumot, ahol az 1. és 2. jószág egyéni értékelése (az ${\displaystyle {\frac {MU_{1}}{MU_{2}}}}$ arány) egyenlő a „piac általi” értékelésével – vagyis a ${\displaystyle {\frac {p_{1}}{p_{2}}}}$ aránnyal.

Sőt, az egyenletet kis átrendezéssel ilyen alakra is hozhatjuk:

${\displaystyle {\frac {MU_{1}}{p_{1}}}={\frac {MU_{2}}{p_{2}}}}$

Ez pedig megfelel a „Gossen II. törvénye” néven ismert, híres közgazdasági összefüggésnek.

Az optimum megváltozása

Jövedelemváltozás hatására

A jövedelemváltozás a költségvetési korlát párhuzamos eltolásával (lásd fent) természetesen az optimum helyét is módosítja.

Az ábrán látható esetben a jövedelemnövekedés hatására mindkét jószágból nőtt az optimális mennyiség. Ez azonban nem minden esetben van így; előfordulhat, hogy az egyik jószág esetében a fogyasztott mennyiség csökkenni fog. Azt a jószágot, amelynek a fogyasztása a jövedelem emelkedésekor növekszik, normál jószágnak, azt pedig, amelynek a mennyisége ilyen esetben csökken, inferior jószágnak nevezzük.

A jövedelemnövekedéssel pontosan ellentétes következményekkel jár a jövedelemcsökkenés.

Ha a különböző jövedelemszintek melletti optimális jószágkombinációkat összekötjük egymással, a két jószág úgynevezett jövedelem-fogyasztási vagy jövedelem-ajánlati görbéjét kapjuk eredményül.

Árváltozás hatására

A jövedelemváltozáshoz hasonlóan itt is csak az egyik esetet, mégpedig az 1. jószág árnövekedését vesszük szemügyre, a másik három – az 1. jószág árcsökkenése, továbbá a 2. jószág áremelkedése és -csökkenése – hasonló változásokat eredményez.

Látnunk kell, hogy p₁ növekedése valójában kétféleképpen is hat a fogyasztásra:

1. Megnő a ${\displaystyle -{\frac {p_{1}}{p_{2}}}}$ hányados, vagyis a költségvetési korlát meredeksége. Ennek a fogyasztásra gyakorolt hatását helyettesítési hatásnak nevezzük.
2. Látszólag a jövedelmünk nem változik, valójában viszont a vásárlóereje csökken, hiszen kevesebb 1. jószágot vásárolhatunk belőle, mint korábban. Ennek következménye az úgynevezett jövedelmi hatás.

A helyettesítési és a jövedelmi hatás összege eredményezi az árváltozás teljes hatását a fogyasztásra. Ezt az összefüggést írja le a Slutsky-egyenlet.

Ha a különböző árszintek melletti optimális jószágkombinációkat kötjük össze egymással, a két jószág ár-fogyasztási vagy ár-ajánlati görbéjét kapjuk meg; ha pedig egyetlen jószág optimális mennyiségét rendeljük a különböző árakhoz, az eredmény a jószág keresleti görbéje vagy keresleti függvénye lesz.

Mikroökonómiai összefüggések segítségével levezethető, hogy árnövekedés esetén a helyettesítési hatás előjele mindig negatív (vagyis az optimális mennyiség csökkenését eredményezi), a jövedelmi hatás viszont lehet negatív és pozitív is, attól függően, hogy normál vagy inferior jószág árnövekedését vizsgáljuk. Így a teljes hatás előjele sem mondható meg egyértelműen; biztosan csak annyit tudunk, hogy normál jószág esetén mindkét hatás negatív, ezért a teljes hatás is az, vagyis normál jószág árnövekedése minden esetben a belőle fogyasztott mennyiség csökkenését eredményezi. Ez a kereslet törvénye.

Fogyasztási döntés indulókészlet mellett

Az eddigiekben feltettük, hogy a fogyasztási döntés előtt álló egyén rendelkezik valamilyen kiinduló jövedelemmel (m), amit javak vásárlására költhet. Megtörténhet azonban az is, hogy a fogyasztónak nincs jövedelme, hanem a javakból van valamilyen indulókészlete, amit aztán addig cserélgethet a környezetével, amíg el nem éri a számára optimális jószágkombinációt.

Kétjószágos modellben a fogyasztó indulókészletét így jelölhetjük: ${\displaystyle (\omega _{1};\omega _{2})\,}$, ahol ω₁ (ómega) az 1. jószág, ω₂ a 2. jószág kiinduló mennyiségét jelenti.

A költségvetési egyenes egyenlete ekkor ilyen lesz:

${\displaystyle p_{1}x_{1}+p_{2}x_{2}=p_{1}\omega _{1}+p_{2}\omega _{2}\,}$

Ekkor az x₁ és x₂ mennyiségeket az 1., illetve a 2. jószág bruttó keresletének nevezzük. Ezzel szemben ${\displaystyle x_{1}-\omega _{1}\,}$ és ${\displaystyle x_{2}-\omega _{2}\,}$ (vagyis a keresett mennyiségeknek a kiinduló mennyiségektől vett eltérése) az 1., illetve a 2. jószág nettó kereslete. (Ha ${\displaystyle x_{1}-\omega _{1}\,}$ vagy ${\displaystyle x_{2}-\omega _{2}\,}$ negatív, akkor nettó kínálatról is beszélhetünk.)

A költségvetési egyenes egyenletét átrendezve kapjuk, hogy

${\displaystyle p_{1}\cdot (x_{1}-\omega _{1})+p_{2}\cdot (x_{2}-\omega _{2})=0.}$

Vagyis a nettó keresleteknek a két jószág árával súlyozott összege 0-val egyenlő. Ez a gyakorlatban azt jelenti, hogy ha a fogyasztó az egyik jószágból a kiinduló mennyiségénél többet akar birtokolni (azaz az egyik jószág nettó vevője szeretne lenni), akkor a másikból mindenképpen el kell adnia valamennyit (tehát a másik jószág nettó eladója kell hogy legyen).

Az optimum megkeresése, valamint a jövedelemváltozás indulókészlet mellett is hasonlóan történik, mint feljebb, csak a jövedelem (m) helyére mindig az indulókészlet értékét (${\displaystyle p_{1}\omega _{1}+p_{2}\omega _{2}\,}$) kell helyettesítenünk. Az árváltozásnál azonban fellép egy harmadik hatás is a helyettesítési és a jövedelmi hatás mellett: az úgynevezett készletjövedelmi hatás. Ez abból ered, hogy árváltozás esetén az indulókészlet értéke – és nemcsak a vásárlóereje – is meg fog változni, ami végső soron a költségvetési korlát és így az optimum eltolódását eredményezi.

Az indulókészletes modell egyik legfontosabb alkalmazása a munkakínálat alapmodellje a munkagazdaságtanban.

Az intertemporális választás

A fogyasztással kapcsolatos döntéseket mindezidáig egy időpontban vizsgáltuk. A valóságban azonban senki sincs arra kötelezve, hogy minden jövedelmét azonnal elköltse; megteheti, hogy eltartalékolja, megtakarítja azt abból a célból, hogy ne a jelenben, hanem a jövőben „cserélje” fogyasztásra. Hasonlóképpen sokféle lehetőség kínálkozik arra, hogy a jelenbeli fogyasztás növelése érdekében kölcsönt vagy hitelt vegyünk fel, amit aztán a jövőbeli jövedelmünkből kell visszafizetnünk. Lehetőségünk van tehát arra, hogy – a jelen- és jövőbeli jövedelmeink által állított korlát figyelembevételével – válasszunk a jelen- és a jövőbeli fogyasztások között. Ezt hívjuk intertemporális választásnak.

Tovább bonyolítja a helyzetet, hogy sem a hitel, sem a megtakarítás nem ingyenes. Ha megtakarítunk valamekkora pénzösszeget, azért a jövőben megkapjuk annak valahány százalékát, az úgynevezett betéti kamatot (a betéti kamatláb jele r_b). Ha hitelt veszünk fel, a jövőben a hitel összege mellett a hitelkamatot (a hitelkamatláb jele r_h) is vissza kell fizetnünk.

A továbbiakban feltételezzük, hogy a megtakarítások és a hitelek piacán is kialakult az egyensúlyi ár, vagyis bármely bankhoz, befektetési vállalathoz stb. fordulunk, mindenhol ugyanazzal a betéti, illetve hitelkamatlábbal szembesülünk.

Az intertemporális választás legegyszerűbb mikroökonómiai modelljében két időpont – vagy időszak –: a jelen és a jövő, és ennek megfelelően két összetett jószág: a jelenbeli fogyasztás (C₁) és a jövőbeli fogyasztás (C₂) szerepel; továbbá az egyszerűség kedvéért feltesszük, hogy ${\displaystyle r_{b}=r_{h}=r\,}$, illetve hogy nincsen infláció. Az indulókészlet ${\displaystyle (M_{1};M_{2})\,}$, ahol M₁ a jelenbeli, M₂ pedig a jövőbeli jövedelem.

A költségvetési egyenes egyenlete ebben az esetben kétféleképpen írható fel. Így:

${\displaystyle C_{1}+{\frac {C_{2}}{1+r}}=M_{1}+{\frac {M_{2}}{1+r}}}$

Vagy pedig így:

${\displaystyle (1+r)\cdot C_{1}+C_{2}=(1+r)\cdot M_{1}+M_{2}}$

Az elsőt a költségvetési egyenes jelenértékes, a másodikat pedig a jövőértékes egyenletének nevezzük. Látható, hogy az egyik egyenlet a másiknak ${\displaystyle 1+r\,}$-szerese, tehát matematikai értelemben nem, csak szemléletükben különböznek egymástól.

Bármelyik egyenletről leolvasható, hogy az intertemporális költségvetési egyenes meredeksége ${\displaystyle -(1+r)\,}$.

Hasonlóan az eddigiekhez, itt is léteznie kell egy ${\displaystyle U(C_{1},C_{2})\,}$ hasznossági függvénynek, amely a jelen- és jövőbeli fogyasztásból álló kombinációkhoz rendel egy-egy számot az intertemporális döntéshozó preferenciáinak megfelelően. Optimális döntés esetén

${\displaystyle {\frac {MU_{C_{1}}}{MU_{C_{2}}}}=1+r.}$

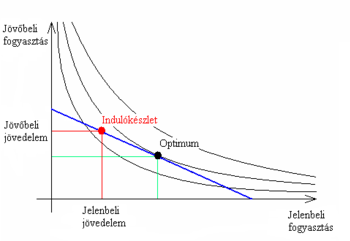
Ha az optimum balra esik az indulókészlettől, akkor az intertemporális döntéshozó kölcsönnyújtó (mivel az első időszakban kevesebbet fogyaszt, mint a jövedelme), ha viszont jobbra, akkor kölcsönvevő.

A fogyasztási döntés általánosabb modellje

Az általánosabb modellben feltesszük, hogy nem kettő, hanem n darab jószág van, amelyek optimális mennyiségéről a fogyasztónak döntést kell hoznia. A választható jószágkosarak ekkor az n dimenziós térben, ${\displaystyle \mathbb {R} ^{n}}$-ben található, nemnegatív koordinátájú vektorokként foghatók fel: ${\displaystyle \mathbf {x} =(x_{1},x_{2},\ldots ,x_{n})}$, ahol x₁ értelemszerűen az első, x₂ a második jószágból fogyasztott mennyiséget reprezentálja, és így tovább. Hasonlóképpen vektorba rendezhetők a javak árai: ${\displaystyle \mathbf {p} =(p_{1},p_{2},\ldots ,p_{n})}$. Az árakat és a jövedelmet (m) természetesen továbbra is külső adottságnak tekintjük, amelyeket a fogyasztó nem képes befolyásolni.

Tegyük fel még, hogy nincsenek adók, támogatások és mennyiségi korlátozások. Ekkor a fogyasztó költségvetési korlátja a következőképpen írható fel:

${\displaystyle p_{1}x_{1}+p_{2}x_{2}+\ldots +p_{n}x_{n}\leq m\,}$

Vagy, a skaláris szorzat definíciójának felhasználásával:

${\displaystyle \mathbf {p} \cdot \mathbf {x} \leq m}$

A költségvetési korlátot leíró egyenlőtlenségből látható, hogy a költségvetési egyenes azon jószágmennyiség-vektorokból áll, amelyeknek az árvektorral vett skalárszorzata éppen m, vagyis olyan n‒1 dimenziós hipersíkot alkot ${\displaystyle \mathbb {R} ^{n}}$-ben, amelynek a normálvektora ${\displaystyle \mathbf {p} }$.

A haszonmaximalizálási feladat és megoldása

A fogyasztó haszonmaximalizálási feladata a következő feltételes szélsőérték-feladat lesz:

${\displaystyle {\begin{matrix}\max U(\mathbf {x} )\\\mathbf {p} \cdot \mathbf {x} \leq m\\\mathbf {x} \geq \mathbf {0} \end{matrix}}}$

Elsőként tegyük fel, hogy egy, az utolsónál szigorúbb feltétel is teljesül: ${\displaystyle \mathbf {x} \gg \mathbf {0} }$, vagyis úgynevezett belső megoldással állunk szemben. Ekkor a feladat ${\displaystyle \mathbf {x^{*}} }$ megoldását – feltéve, hogy U differenciálható függvény – a Kuhn-Tucker feltételek szerint a következő egyenletrendszer gyökei fogják szolgáltatni (${\displaystyle MU_{i}\,}$ továbbra is a hasznossági függvény i-edik változója szerinti parciális deriváltját jelöli):

${\displaystyle {\begin{matrix}MU_{1}(\mathbf {x^{*}} )-\lambda p_{1}=0\\MU_{2}(\mathbf {x^{*}} )-\lambda p_{2}=0\\\vdots \\MU_{n}(\mathbf {x^{*}} )-\lambda p_{n}=0\\\mathbf {p} \cdot \mathbf {x^{*}} -m=0\end{matrix}}}$

A határhasznokra vonatkozó egyenletek másként, vektoregyenlet alakban:

${\displaystyle \nabla U(\mathbf {x^{*}} )-\lambda \mathbf {p} =\mathbf {0} }$,

ahol ${\displaystyle \nabla U(\mathbf {x} )}$ a hasznossági függvény gradiense (a függvény parciális deriváltjaiból álló vektor). Átrendezve:

${\displaystyle \nabla U(\mathbf {x^{*}} )=\lambda \mathbf {p} }$,

vagyis ott találunk optimumot, ahol a hasznossági függvény gradiensvektora párhuzamos a költségvetési korlát normálvektorával. Ez az állítás a kétjószágos modellben megismert érintési feltétel általánosításának tekinthető.

Az előbbi feltétel szükséges, de nem elégséges a belső optimum létezéséhez. Vannak bizonyos másodrendű feltételek is, amelyek a hasznossági függvény kvázikonkavitásával kapcsolatosak. Az elsőrendű feltételt kielégítő ${\displaystyle \mathbf {x^{*}} }$ megoldásvektor pontosan akkor lokális maximumhely, ha a hasznossági függvény ${\displaystyle \mathbf {x^{*}} }$-ban kvázikonkáv. Ha pedig U értelmezési tartományának egészén kvázikonkáv, akkor az elsőrendű feltételt kielégítő ${\displaystyle \mathbf {x^{*}} }$ globálisan is maximumhely, vagyis a haszonmaximalizálási feladat megoldása.

Ha a fenti egyenletek mindegyikéből kifejezzük ${\displaystyle \lambda \,}$-t, ezúttal is Gossen II. törvényét kapjuk:

${\displaystyle \lambda ={\frac {MU_{1}(\mathbf {x^{*}} )}{p_{1}}}={\frac {MU_{2}(\mathbf {x^{*}} )}{p_{2}}}=\ldots ={\frac {MU_{n}(\mathbf {x^{*}} )}{p_{n}}}}$

Ha a haszonmaximalizálási feladat ${\displaystyle \mathbf {x^{*}} }$ megoldása nem belső megoldás, vagyis van legalább egy olyan jószág, amiből a fogyasztó semennyit sem fogyaszt az optimumban (ez valószerű feltevés), akkor az egyenletrendszer a Kuhn–Tucker-féle korlátozó feltételeknek megfelelően következőképpen módosul:

${\displaystyle \nabla U(\mathbf {x^{*}} )-\lambda \mathbf {p} \leq \mathbf {0} }$,

és azokra a javakra, amelyekre ${\displaystyle x_{i}^{*}>0}$, tehát amelyekből az optimális fogyasztás pozitív,

${\displaystyle MU_{i}(\mathbf {x^{*}} )-\lambda p_{i}=0}$.

A megoldás létezése és egyértelműsége

Ha a javak árai kivétel nélkül pozitívak, azaz ${\displaystyle \mathbf {p} \gg \mathbf {0} }$, továbbá a jövedelem nemnegatív, akkor a fogyasztó által választható (tehát nemnegatív és a költségvetési korlátot kielégítő) jószágkosarak halmaza, amit korábban költségvetési halmaznak neveztünk, nemüres, zárt és korlátos. Ekkor a hasznossági függvény folytonossága esetén a Weierstrass-tétel biztosítja, hogy a haszonmaximalizálási feladatnak minden, a feltételnek megfelelő árvektor és jövedelem mellett létezik megoldása.

Definiálható tehát egy leképezés, amely valamely árvektor–jövedelem kombinációhoz az ezek mellett optimális jószágkosarak halmazát rendeli. Ezt a leképezést (marshalli vagy walrasi) keresleti leképezésnek nevezhetjük és a következőképpen jelöljük: ${\displaystyle \mathbf {x} (\mathbf {p} ,m)}$.

Ha a megoldás létezését biztosító feltételeken kívül teljesül még, hogy a fogyasztó preferenciái konvexek (vagy, ami ezzel egyenértékű: a hasznossági függvény kvázikonkáv), akkor az ${\displaystyle \mathbf {x} (\mathbf {p} ,m)}$ halmaz minden ${\displaystyle (\mathbf {p} ,m)}$-re konvex. Ha pedig a preferenciák szigorúan konvexek (a hasznossági függvény szigorúan kvázikonkáv), akkor az ${\displaystyle \mathbf {x} (\mathbf {p} ,m)}$ halmaz minden árvektor–jövedelem kombinációra egyelemű, vagyis a leképezés egyértelmű: ${\displaystyle \mathbf {x} (\mathbf {p} ,m)}$ egy ${\displaystyle \mathbb {R} ^{n+1}}$-ből ${\displaystyle \mathbb {R} ^{n}}$-be képező függvény, amit keresleti függvénynek nevezhetünk (ráadásul belátható, hogy ez a függvény folytonos). A továbbiakban minden esetben feltételezzük, hogy fennállnak a keresleti függvény létezéséhez szükséges feltételek.

A keresleti függvény tulajdonságai

Igazolható, hogy a haszonmaximalizálási feladat megoldásaként adódó keresleti függvény minden esetben teljesíti az alábbi tulajdonságokat:

1. ${\displaystyle \mathbf {p} \cdot \mathbf {x} (\mathbf {p} ,m)=m}$ (Walras-törvénye), a preferenciák lokális telíthetetlensége, ill. monotonitása következményeként.
2. Minden pozitív t valós számra ${\displaystyle \mathbf {x} (t\mathbf {p} ,tm)=\mathbf {x} (\mathbf {p} ,m)}$, vagyis a keresleti függvény nulladfokon homogén.
3. Jelölje a keresleti függvény i-edik koordinátafüggvényét (vagyis az i-edik jószág keresletét az árak és a jövedelem függvényében) ${\displaystyle x_{i}(\mathbf {p} ,m)}$. Ekkor az ${\displaystyle s_{i,j}={\frac {\partial x_{i}(\mathbf {p} ,m)}{\partial p_{j}}}+{\frac {\partial x_{i}(\mathbf {p} ,m)}{\partial m}}\cdot x_{j}(\mathbf {p} ,m)}$ elemekből álló n×n-es mátrix, az úgynevezett helyettesítési mátrix vagy Slutsky-mátrix szimmetrikus, negatív szemidefinit, és nem teljes rangú.

Az eddig leírtaknál erősebb állítás is megfogalmazható: ha egy ${\displaystyle \mathbf {x} (\mathbf {p} ,m)}$ függvényre teljesül a fenti három tulajdonság, akkor létezik olyan preferenciarendszer (hasznossági függvény), amelynek ${\displaystyle \mathbf {x} (\mathbf {p} ,m)}$ a keresleti függvénye.

Az indirekt hasznossági függvény

Az indirekt hasznossági függvény a haszonmaximalizálási feladat értékfüggvénye, vagyis minden árvektor–jövedelem kombinációhoz az ezek mellett optimális jószágkombináció(k) hasznosságát rendeli:

${\displaystyle v(\mathbf {p} ,m)=U(\mathbf {x} (\mathbf {p} ,m))}$

Az indirekt hasznossági függvény a következő tulajdonságokkal rendelkezik:

1. Nulladfokon homogén: minden pozitív valós t-re ${\displaystyle v(t\mathbf {p} ,tm)=v(\mathbf {p} ,m)}$.
2. Nemnövekvő az árakban: ${\displaystyle \mathbf {p'} \geq \mathbf {p} }$ esetén ${\displaystyle v(\mathbf {p'} ,m)\leq v(\mathbf {p} ,m)}$.
3. Szigorúan növekvő a jövedelemben: ha ${\displaystyle m'>m\,}$, akkor ${\displaystyle v(\mathbf {p} ,m')>v(\mathbf {p} ,m)}$.
4. Kvázikonvex.
5. Folytonos.

A Roy-azonosság az indirekt hasznossági függvény definíciójával ellentétes irányú kapcsolatot teremt az indirekt hasznossági függvény és a keresleti függvény között. Kimondja, hogy ${\displaystyle v(\mathbf {p} ,m)}$ differenciálhatósága esetén minden i-re

${\displaystyle x_{i}(\mathbf {p} ,m)=-{\frac {\frac {\partial v(\mathbf {p} ,m)}{\partial p_{i}}}{\frac {\partial v(\mathbf {p} ,m)}{\partial m}}}}$.

Források

• Varian, H. R. (2005), Mikroökonómia középfokon, Akadémiai Kiadó, ISBN 963-05-8308-9
• Mas-Colell, Andreu; Whinston, Michael; Green, Jerry (1995): Microeconomic Theory. Oxford: Oxford University Press. ISBN 0-19-507340-1