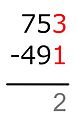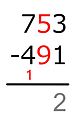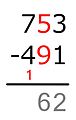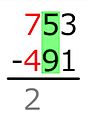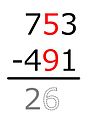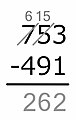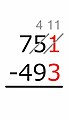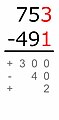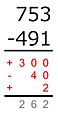Pengurangan

Operasi aritmetika l b s

Penambahan (+) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{suku}}\,+\,{\text{suku}}\\\scriptstyle {\text{yang ditambah}}\,+\,{\text{penambah}}\\\scriptstyle {\text{tinambah}}\,+\,{\text{penambah}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{jumlah}}}$ Pengurangan (−) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{suku}}\,-\,{\text{suku}}\\\scriptstyle {\text{kinurang}}\,-\,{\text{pengurang}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle {\begin{matrix}\scriptstyle {\text{selisih}}\\\scriptstyle {\text{beda}}\end{matrix}}}$ Perkalian (×) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{faktor}}\,\times \,{\text{faktor}}\\\scriptstyle {\text{pengali}}\,\times \,{\text{kinali}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle {\begin{matrix}\scriptstyle {\text{hasil kali}}\\\scriptstyle {\text{darab}}\end{matrix}}}$ Pembagian (÷), (/) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\frac {\scriptstyle {\text{dividen}}}{\scriptstyle {\text{pembagi}}}}\\\scriptstyle {\text{ }}\\\scriptstyle {\frac {\scriptstyle {\text{pembilang}}}{\scriptstyle {\text{penyebut}}}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle {\begin{matrix}\scriptstyle {\text{hasil bagi}}\\\scriptstyle {\text{pecahan}}\\\scriptstyle {\text{rasio}}\end{matrix}}}$ Eksponensiasi (^) ${\displaystyle \scriptstyle {\text{bilangan pokok}}^{\text{eksponen}}\,=\,}$ ${\displaystyle \scriptstyle {\text{pangkat}}}$ Penarikan akar (√) ${\displaystyle \scriptstyle {\sqrt[{\text{pangkat}}]{\scriptstyle {\text{radikan}}}}\,=\,}$ ${\displaystyle \scriptstyle {\text{akar}}}$ Logaritma (log) ${\displaystyle \scriptstyle ^{\text{bilangan pokok}}\!\log({\text{antilogaritma}})\,=\,}$ ${\displaystyle \scriptstyle {\text{logaritma}}}$

Operasi aritmetika l b s

Penambahan (+) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{suku}}\,+\,{\text{suku}}\\\scriptstyle {\text{yang ditambah}}\,+\,{\text{penambah}}\\\scriptstyle {\text{tinambah}}\,+\,{\text{penambah}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{jumlah}}}$ Pengurangan (−) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{suku}}\,-\,{\text{suku}}\\\scriptstyle {\text{kinurang}}\,-\,{\text{pengurang}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle {\begin{matrix}\scriptstyle {\text{selisih}}\\\scriptstyle {\text{beda}}\end{matrix}}}$ Perkalian (×) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{faktor}}\,\times \,{\text{faktor}}\\\scriptstyle {\text{pengali}}\,\times \,{\text{kinali}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle {\begin{matrix}\scriptstyle {\text{hasil kali}}\\\scriptstyle {\text{darab}}\end{matrix}}}$ Pembagian (÷), (/) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\frac {\scriptstyle {\text{dividen}}}{\scriptstyle {\text{pembagi}}}}\\\scriptstyle {\text{ }}\\\scriptstyle {\frac {\scriptstyle {\text{pembilang}}}{\scriptstyle {\text{penyebut}}}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle {\begin{matrix}\scriptstyle {\text{hasil bagi}}\\\scriptstyle {\text{pecahan}}\\\scriptstyle {\text{rasio}}\end{matrix}}}$ Eksponensiasi (^) ${\displaystyle \scriptstyle {\text{bilangan pokok}}^{\text{eksponen}}\,=\,}$ ${\displaystyle \scriptstyle {\text{pangkat}}}$ Penarikan akar (√) ${\displaystyle \scriptstyle {\sqrt[{\text{pangkat}}]{\scriptstyle {\text{radikan}}}}\,=\,}$ ${\displaystyle \scriptstyle {\text{akar}}}$ Logaritma (log) ${\displaystyle \scriptstyle ^{\text{bilangan pokok}}\!\log({\text{antilogaritma}})\,=\,}$ ${\displaystyle \scriptstyle {\text{logaritma}}}$

Pengurangan adalah operasi aritmetika yang mewakili operasi menghapus objek dari koleksi. Pengurangan ditandai dengan tanda minus, −. Misalnya, pada gambar di sebelahnya, 5 − 2 buah persik—artinya 5 buah persik dengan 2 buah yang diambil, menghasilkan total 3 buah persik. Oleh karena itu, selisih dari 5 dan 2 adalah 3; yaitu, 5 − 2 = 3. Sementara terutama terkait dengan bilangan asli di aritmetika, pengurangan juga mewakili penghapusan atau pengurangan kuantitas fisik dan abstrak menggunakan berbagai jenis objek termasuk bilangan negatif, pecahan, bilangan irasional, vektor, desimal, fungsi, dan matriks.^[1][2]

Pengurangan mengikuti beberapa pola penting. Ini adalah antikomutatif, artinya mengubah urutan mengubah tanda jawaban. Ini juga bukan asosiasi, artinya ketika mengurangi lebih dari dua angka, urutan pengurangan dilakukan penting. Karena 0 adalah identitas aditif, pengurangannya tidak mengubah angka. Pengurangan juga mematuhi aturan yang diprediksi mengenai operasi terkait, seperti penambahan dan perkalian. Semua aturan ini dapat menjadi pembuktian, dimulai dengan pengurangan bilangan bulat dan digeneralisasi melalui bilangan riil dan seterusnya. Operasi biner umum yang mengikuti pola ini dipelajari di aljabar abstrak.

Melakukan pengurangan pada bilangan asli adalah salah satu tugas numerik paling sederhana. Pengurangan angka yang kecil dapat diakses oleh anak kecil. Dalam pendidikan dasar misalnya, siswa diajarkan untuk mengurangi angka dalam sistem desimal, dimulai dengan satu digit dan secara progresif menangani masalah yang lebih sulit.

Dalam aljabar lanjutan dan aljabar komputer, ekspresi yang melibatkan pengurangan seperti A − B umumnya sebagai notasi singkatan untuk penambahan A + (−B). Jadi, A − B mengandung dua suku, yaitu A dan −B. Ini memungkinkan penggunaan asosiasi dan komutatif yang lebih mudah.

Notasi

Pengurangan biasanya ditulis menggunakan tanda minus "−" di antara suku;^[3] yaitu, dalam notasi infiks. Hasilnya dinyatakan dengan tanda sama dengan. Sebagai contoh,

${\displaystyle 2-1=1}$ (diucapkan sebagai "dua dikurangi satu sama dengan satu")

${\displaystyle 4-2=2}$ (diucapkan sebagai "empat dikurangi dua sama dengan dua")

${\displaystyle 6-3=3}$ (diucapkan sebagai "enam dikurangi tiga sama dengan tiga")

${\displaystyle 4-6=-2}$ (diucapkan sebagai "empat dikurangi enam sama dengan negatif dua")

Ada juga situasi dimana pengurangan "dipahami", meskipun tidak ada simbol yang muncul:

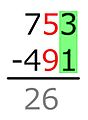
• Kolom dua angka, dengan angka yang lebih rendah berwarna merah, biasanya menunjukkan bahwa angka yang lebih rendah dalam kolom tersebut harus dikurangi, dengan perbedaan yang ditulis di bawah, di bawah garis. Ini paling umum dalam akuntansi.

Secara formal, angka yang dikurangi dikenal sebagai pengurangan,^[4][5] sedangkan angka yang dikuranginya adalah minuend.^[4][5] Hasilnya adalah beda.^[2][4][5][6]

Dari bilangan bulat dan bilangan riil

Bilangan bulat

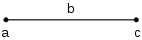
Bayangkan sebuah segmen garis dari panjang b dengan ujung kiri berlabel a dan ujung kanan berlabel c. Dimulai dari a, dibutuhkan langkah b ke kanan untuk mencapai c. Pergerakan ke kanan ini dimodelkan secara matematis oleh penambahan:

a + b = c.

Dari c, dibutuhkan b langkah ke kiri untuk kembali ke a. Gerakan ke kiri ini dimodelkan dengan pengurangan:

c − b = a.

Sekarang, segmen garis berlabel 1, 2, dan 3. Dari posisi 3, tidak perlu mengambil langkah ke kiri untuk tetap di 3, jadi 3 − 0 = 3. Dibutuhkan 2 langkah ke kiri untuk sampai ke posisi 1, jadi 3 − 2 = 1. Gambar ini tidak cukup untuk menggambarkan apa yang akan terjadi setelah 3 langkah ke kiri dari posisi 3. Untuk mewakili operasi seperti itu, garis harus diperpanjang.

Untuk mengurangi bilangan asli arbitrer, satu dimulai dengan garis yang berisi setiap bilangan asli (0, 1, 2, 3, 4, 5, 6, ...). Dari 3, dibutuhkan 3 langkah ke kiri untuk sampai ke 0, jadi 3 − 3 = 0. Tetapi 3 − 4 masih tidak valid, karena meninggalkan barisan. Bilangan asli bukanlah konteks yang berguna untuk pengurangan.

Solusinya adalah dengan mempertimbangkan bilangan bulat garis bilangan (..., 3, 2, 1, 0, 1, 2, 3, ...). Dengan cara ini, dibutuhkan 4 langkah ke kiri dari 3 untuk sampai ke 1:

3 − 4 = −1.

Bilangan asli

Pengurangan bilangan asli bukan tertutup: selisihnya bukan bilangan asli kecuali jika minuend lebih besar dari atau sama dengan pengurangan. Misalnya, 26 tidak dapat dikurangkan dari 11 untuk menghasilkan bilangan asli. Kasus seperti itu menggunakan salah satu dari dua pendekatan:

1. Simpulkan bahwa 26 tidak dapat dikurangkan dari 11; pengurangan menjadi fungsi parsial.
2. Berikan jawabannya sebagai bilangan bulat yang mewakili bilangan negatif, sehingga hasil pengurangan 26 dari 11 adalah −15.

Bilangan riil

Medan bilangan riil didefinisikan dengan menentukan hanya dua operasi biner, penjumlahan dan perkalian, bersama-sama dengan operasi uner menghasilkan invers penjumlahan dan perkalian. Pengurangan bilangan riil (pengurang) dari yang lain (minuend) didefinisikan sebagai penambahan minuend dan invers aditif dari pengurangan. Misalnya, 3 − π = 3 + (−π). Sebagai alternatif, alih-alih memerlukan operasi uner ini, operasi biner dari pengurangan dan pembagian dapat diambil sebagai dasar.

Sifat

Antikomutatif

Pengurangan adalah anti-komutatif, artinya jika kita membalik suku-suku dalam selisih kiri-ke-kanan, hasilnya adalah negatif dari hasil semula. Secara simbolis, jika a dan b adalah dua bilangan, maka

a − b = −(b − a).

Non-asosiasi

Pengurangan adalah non-asosiatif, yang muncul seketika mencoba mendefinisikan pengurangan berulang. Secara umum, ekspresi

"a − b − c"

apabila didefinisikan berarti (a − b) − c atau a − (b − c), tetapi dua kemungkinan ini menyebabkan jawaban yang berbeda. Untuk mengatasi masalah ini, apabila membuat urutan operasi, dengan perintah yang berbeda menghasilkan hasil yang berbeda.

Pendahulu

Dalam konteks bilangan bulat, pengurangan satu juga memainkan peran khusus: untuk sembarang bilangan bulat a, bilangan bulat (a − 1) adalah bilangan bulat terbesar yang kurang dari a, juga dikenal sebagai pendahulu a.

Satuan pengukuran

Saat mengurangkan dua angka dengan satuan ukuran seperti kilogram atau pon, keduanya harus memiliki satuan yang sama. Dalam kebanyakan kasus, selisihnya akan memiliki satuan yang sama dengan bilangan aslinya.

Persentase

Perubahan persentase apabila dilaporkan dalam setidaknya dua bentuk, perubahan persentase dan perubahan titik persentase. Perubahan persentase mewakili perubahan relatif antara dua kuantitas sebagai persentase, sementara perubahan titik persentase hanyalah angka yang diperoleh dengan mengurangkan dua persentase.^[7][8][9]

Sebagai contoh, anggaplah 30% widget yang dibuat di pabrik rusak. Enam bulan kemudian, 20% widget rusak. Perubahan persentase adalah 20% − 30%30% = −13 = −33 13%, sedangkan perubahan poin persentase adalah 10 titik persentase.

Dalam komputasi

Metode komplemen adalah teknik yang digunakan untuk mengurangkan satu bilangan dari bilangan lain hanya dengan menggunakan penjumlahan bilangan positif. Metode ini biasa digunakan di kalkulator mekanis, dan masih digunakan di komputer modern.

Untuk mengurangkan bilangan biner y (pengurang) dari bilangan lain x (minuend), komplemen satu dari y ditambahkan ke x dan satu ditambahkan ke jumlah. Digit terdepan "1" dari hasil kemudian dibuang.

Metode komplemen sangat berguna dalam biner (akar 2) karena komplemen satu sangat mudah diperoleh dengan membalik setiap bit (mengubah "0" menjadi "1" dan sebaliknya). Dan menambahkan 1 untuk mendapatkan komplemen keduanya dapat dilakukan dengan mensimulasikan carry ke bit yang paling tidak signifikan. Sebagai contoh:

  01100100  (x, sama dengan desimal 100)
- 00010110 (y, sama dengan desimal 22)

menjadi jumlah:

  01100100  (x)
+ 11101001  (pelengkap satu dari y)
+        1  (untuk mendapatkan komplemen keduanya)
——————————
 101001110

Menjatuhkan awal "1" memberikan jawabannya: 01001110 (sama dengan desimal 78)

Pengajaran pengurangan di sekolah

Metode yang digunakan untuk mengajarkan pengurangan ke sekolah dasar bervariasi dari satu negara ke negara lain, dan di dalam suatu negara, metode yang berbeda diadopsi pada waktu yang berbeda. Dalam apa yang dikenal di Amerika Serikat sebagai matematika tradisional, proses tertentu diajarkan kepada siswa pada akhir tahun ke-1 (atau selama tahun ke-2) untuk digunakan dengan bilangan bulat multi-digit, dan diperluas baik di kelas empat atau lima untuk memasukkan representasi desimal bilangan pecahan.

Di Amerika

Hampir semua sekolah Amerika saat ini mengajarkan metode pengurangan menggunakan peminjaman atau pengelompokan ulang (algoritma dekomposisi) dan sistem penandaan yang disebut kruk.^[10][11] Meskipun metode peminjaman telah dikenal dan diterbitkan dalam buku teks sebelumnya, penggunaan kruk di sekolah-sekolah Amerika menyebar setelah William A. Brownell menerbitkan sebuah penelitian—mengklaim bahwa kruk bermanfaat bagi siswa yang menggunakan metode ini.^[12] Sistem ini berkembang pesat, menggantikan metode pengurangan lain yang digunakan di Amerika pada waktu itu.

Di Eropa

Beberapa sekolah Eropa menggunakan metode pengurangan yang disebut metode Austria, juga dikenal sebagai metode penambahan. Tidak ada pinjaman dalam metode ini. Ada juga kruk (tanda untuk membantu ingatan), yang berbeda-beda di setiap negara.^[13][14]

Membandingkan dua metode utama

Kedua metode ini memecah pengurangan sebagai proses pengurangan satu digit berdasarkan nilai tempat. Dimulai dengan angka yang paling tidak signifikan, pengurangan dari pengurangan:

s_j s_j−1 ... s₁

dari minuend

m_k m_k−1 ... m₁,

dimana s_i dan m_i adalah angka, lanjutkan dengan menuliskan m₁ − s₁, m₂ − s₂, dan seterusnya, selama s_i tidak melebihi m_i. Jika tidak, m_i bertambah 10 dan beberapa digit lainnya dimodifikasi untuk mengoreksi kenaikan ini. Metode Amerika mengoreksi dengan mencoba mengurangi digit minuend m_i+1 per satu (atau melanjutkan peminjaman ke kiri sampai ada angka bukan nol untuk meminjam). Metode Eropa mengoreksi dengan menambah satu digit subtrahend s_i+1.

Contoh: 704 − 512.

${\displaystyle {\begin{array}{rrrr}&\color {Red}-1\\&C&D&U\\&7&0&4\\&5&1&2\\\hline &1&9&2\\\end{array}}{\begin{array}{l}{\color {Red}\longleftarrow {\rm {penerus}}}\\\\\longleftarrow \;{\rm {Minuend}}\\\longleftarrow \;{\rm {Pengurangan}}\\\longleftarrow {\rm {Hasil\;atau\;Beda}}\\\end{array}}}$

Minuend adalah 704, pengurangan adalah 512. Digit minuend adalah m₃ = 7, m₂ = 0 dan m₁ = 4. Digit pengurangan adalah s₃ = 5, s₂ = 1 dan s₁ = 2. Mulai dari tempat satu, 4 tidak kurang dari 2 jadi selisih 2 ditulis di tempat hasil. Di tempat sepuluh, 0 kurang dari 1, jadi 0 bertambah 10, dan selisihnya dengan 1, yaitu 9, ditulis di tempat sepuluh. Metode Amerika mengoreksi kenaikan sepuluh dengan mengurangi angka di tempat ratusan minuend satu per satu. Artinya, 7 dipukul dan diganti dengan 6. Pengurangan kemudian dilanjutkan di tempat ratusan, di mana 6 tidak kurang dari 5, jadi selisihnya ditulis di tempat hasil ratusan. Kita sekarang selesai, hasilnya adalah 192.

Metode Austria tidak mengurangi 7 menjadi 6. Melainkan menambah satu digit pengurangan seratus. Sebuah tanda kecil dibuat di dekat atau di bawah angka ini (tergantung pada sekolah). Kemudian pengurangan dilanjutkan dengan menanyakan bilangan berapa bila ditambah 1, dan 5 dijumlahkan menjadi 7. Jawabannya adalah 1, dan hasilnya ditulis di tempat ratusan.

Ada kehalusan tambahan bahwa siswa selalu menggunakan tabel pengurangan mental dalam metode Amerika. Metode Austria sering mendorong siswa untuk secara mental menggunakan tabel penjumlahan secara terbalik. Dalam contoh di atas, daripada menjumlahkan 1 hingga 5, mendapatkan 6, dan mengurangkannya dari 7, siswa diminta untuk mempertimbangkan bilangan apa, ketika ditambah 1, dan 5 ditambahkan, menjadi 7.

Pengurangan dengan tangan

Metode Austria

Contoh:

• 
  1 + ... = 3
• 
  Perbedaannya ditulis di bawah garis.
• 
  9 + ... = 5
  Jumlah yang diperlukan (5) terlalu kecil.
• 
  Jadi, kita menambahkan 10 dan menempatkan 1 di bawah tempat yang lebih tinggi berikutnya di pengurangan.
• 
  9 + ... = 15
  Sekarang kita dapat menemukan perbedaan seperti sebelumnya.
• 
  (4 + 1) + ... = 7
• 
  Perbedaannya ditulis di bawah garis.
• 
  Perbedaan/Hasil total.

Pengurangan dari kiri ke kanan

Contoh:

• 
  7 − 4 = 3
  Hasil ini hanya dengan pensil.
• 
  Karena digit berikutnya dari minuend lebih kecil dari subtrahend, kita kurangi satu dari nomor pensil kita dan secara mental tambahkan sepuluh ke yang berikutnya.
• 
  15 − 9 = 6
• 
  Karena digit berikutnya di minuend tidak lebih kecil dari subtrahend, Kami menyimpan nomor ini.
• 
  3 − 1 = 2

Metode Amerika

Dalam metode ini, setiap digit pengurangan dikurangi dari digit di atasnya mulai dari kanan ke kiri. Jika angka atas terlalu kecil untuk mengurangi angka bawah dari itu, kami menambahkan 10 untuk itu; 10 ini "dipinjam" dari digit atas ke kiri, yang kita kurangi 1 darinya. Kemudian kita beralih ke pengurangan digit berikutnya dan meminjam sesuai kebutuhan, sampai setiap digit telah dikurangi. Contoh:

• 
  3 − 1 = ...
• 
  Kita menulis perbedaan di bawah garis.
• 
  5 − 9 = ...
  Minuend (5) terlalu kecil!
• 
  Jadi, kita menambahkan 10 untuk itu. Angka 10 "dipinjam" dari angka di sebelah kiri, yang turun 1.
• 
  15 − 9 = ...
  Sekarang pengurangan bekerja, dan kita menulis perbedaan di bawah garis.
• 
  6 − 4 = ...
• 
  Kita menulis perbedaan di bawah garis.
• 
  Perbedaan/Hasil total.

Hasil tukar

Varian dari metode dimana semua peminjaman dilakukan sebelum semua pengurangan.^[15]

Contoh:

• 
  1 − 3 = tidak mungkin.
  Kita menambahkan 10 ke 1. Karena 10 "dipinjam" dari 5 terdekat, 5 dikurangi 1.
• 
  4 – 9 = tidak mungkin.
  Jadi kita lanjutkan seperti pada langkah 1.
• 
  Dimulai dari kanan ke kiri:
  11 − 3 = 8
• 
  14 − 9 = 5
• 
  6 − 4 = 2

Selisih parsial

Metode perbedaan parsial berbeda dari metode pengurangan vertikal lainnya karena tidak ada peminjaman atau pengangkutan yang terjadi. Di tempat ini, satu tempat tanda plus atau minus tergantung pada apakah minuend lebih besar atau lebih kecil dari subtrahend. Jumlah dari perbedaan parsial adalah perbedaan total.^[16]

Contoh:

• 
  Angka yang lebih kecil dikurangi dari yang lebih besar:
  700 − 400 = 300
  Karena minuend lebih besar dari subtrahend, perbedaan ini memiliki tanda plus.
• 
  Angka yang lebih kecil dikurangi dari yang lebih besar:
  90 − 50 = 40
  Karena minuend lebih kecil dari subtrahend, perbedaan ini memiliki tanda minus.
• 
  Angka yang lebih kecil dikurangi dari yang lebih besar:
  3 − 1 = 2
  Karena minuend lebih besar dari subtrahend, perbedaan ini memiliki tanda plus.
• 
  +300 − 40 + 2 = 262

Metode non-vertikal

Menghitung

Alih-alih menemukan selisih digit demi digit, apabila menghitung angka antara pengurangan dan minuend.^[17]

Contoh: 1234 − 567 = dapat ditemukan dengan langkah-langkah berikut:

• 567 + 3 = 570
• 570 + 30 = 600
• 600 + 400 = 1000
• 1000 + 234 = 1234

Jumlahkan nilai dari setiap langkah untuk mendapatkan selisih total: 3 + 30 + 400 + 234 = 667.

Memutus pengurangan

Metode lain yang berguna untuk mental aritmetika adalah dengan membagi pengurangan menjadi langkah-langkah kecil.^[18]

Contoh: 1234 − 567 = dapat diselesaikan dengan cara berikut:

• 1234 − 500 = 734
• 734 − 60 = 674
• 674 − 7 = 667

Perubahan yang sama

Metode perubahan yang sama menggunakan fakta bahwa menambahkan atau mengurangi angka yang sama dari minuend dan pengurangan tidak mengubah jawabannya. Cukup menambahkan jumlah yang dibutuhkan untuk mendapatkan nol dalam pengurangan.^[19]

Contoh:

"1234 − 567 =" dapat diselesaikan sebagai berikut:

• 1234 − 567 = 1237 − 570 = 1267 − 600 = 667

Lihat pula

• Pengurangan
• Aritmetika dasar
• Metode komplemen
• Bilangan negatif
• Tanda plus dan minus

Referensi

Bibliografi

• Brownell, W.A. (1939). Learning as reorganization: An experimental study in third-grade arithmetic, Duke University Press.
• Subtraction in the United States: An Historical Perspective, Susan Ross, Mary Pratt-Cotter, The Mathematics Educator, Vol. 8, No. 1 (original publication) and Vol. 10, No. 1 (reprint.) PDF

Pranala luar

Lihat entri pengurangan di kamus bebas Wiktionary.