Distribuzione Beta

Niente fonti!
Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti.
Commento: voce totalmente priva di fonti
Distribuzione B ( α , β ) {\displaystyle \mathrm {B} (\alpha ,\beta )}
Funzione di densità di probabilità
Funzione di densità di probabilità
Funzione di ripartizione
Funzione di ripartizione
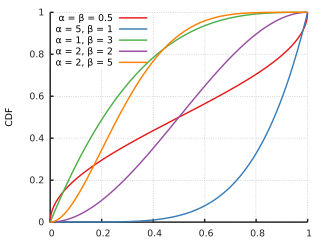Parametri α , β > 0   {\displaystyle \alpha ,\beta >0\ }
Supporto [ 0 , 1 ]   {\displaystyle [0,1]\ }
Funzione di densità x α − 1 ( 1 − x ) β − 1 B ( α , β ) {\displaystyle {\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}}
Funzione di ripartizione I x ( α , β )   {\displaystyle I_{x}(\alpha ,\beta )\ }
(funzione Beta incompleta regolarizzata)
Valore atteso α α + β {\displaystyle {\frac {\alpha }{\alpha +\beta }}}
Moda α − 1 α + β − 2 {\displaystyle {\frac {\alpha -1}{\alpha +\beta -2}}} se α , β > 1   {\displaystyle \alpha ,\beta >1\ }


0   {\displaystyle 0\ } se α < 1   {\displaystyle \alpha <1\ } e β ⩾ 1 {\displaystyle \beta \geqslant 1}
1   {\displaystyle 1\ } se α ⩾ 1 {\displaystyle \alpha \geqslant 1} e β < 1   {\displaystyle \beta <1\ }

Varianza α β ( α + β ) 2 ( α + β + 1 ) {\displaystyle {\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}}
Indice di asimmetria 2 β − α α + β + 2 α + β + 1 α β {\displaystyle 2{\frac {\beta -\alpha }{\alpha +\beta +2}}{\sqrt {\frac {\alpha +\beta +1}{\alpha \beta }}}}
Funzione generatrice dei momenti 1 + ∑ k = 1 ∞ ( ∏ r = 0 k − 1 α + r α + β + r ) t k k ! {\displaystyle 1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{k}}{k!}}}
Funzione caratteristica 1 F 1 ( α ; α + β ; i t ) {\displaystyle {}_{1}F_{1}(\alpha ;\alpha +\beta ;i\,t)}
Manuale

In teoria delle probabilità e in statistica, la distribuzione B {\displaystyle \mathrm {B} } (Beta) è una distribuzione di probabilità continua definita da due parametri α {\displaystyle \alpha } e β {\displaystyle \beta } sull'intervallo unitario [ 0 , 1 ] {\displaystyle [0,1]} .

Questa distribuzione nasce in modo molto naturale nella inferenza bayesiana, perché governa la probabilità p {\displaystyle p} di un processo di Bernoulli a posteriori dell'osservazione di α − 1 {\displaystyle \alpha -1} "successi" e β − 1 {\displaystyle \beta -1} "fallimenti", quando p {\displaystyle p} è a priori distribuita uniformemente tra 0 {\displaystyle 0} e 1 {\displaystyle 1} .

Definizione

La distribuzione Beta di parametri ( α , β ) {\displaystyle (\alpha ,\beta )} (entrambi positivi) è definita sull'intervallo [ 0 , 1 ] {\displaystyle [0,1]} con funzione di densità di probabilità

f ( x ) = x α − 1 ( 1 − x ) β − 1 B ( α , β ) {\displaystyle f(x)={\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}} .

In altri termini la funzione di densità di probabilità è proporzionale alla funzione

x α − 1 ( 1 − x ) β − 1 {\displaystyle x^{\alpha -1}(1-x)^{\beta -1}} ,

riscalata per un fattore dato dalla funzione Beta

B ( α , β ) = ∫ 0 1 x α − 1 ( 1 − x ) β − 1 d x {\displaystyle \mathrm {B} (\alpha ,\beta )=\int _{0}^{1}x^{\alpha -1}(1-x)^{\beta -1}dx} ;

in questo modo ha probabilità totale P ( X ∈ [ 0 , 1 ] ) = 1 {\displaystyle P(X\in [0,1])=1} .

La sua funzione di ripartizione è la funzione Beta incompleta regolarizzata

F ( x ) = I x ( α , β ) = B x ( α , β ) B ( α , β ) = ∫ 0 x t α − 1 ( 1 − t ) β − 1 d t ∫ 0 1 t α − 1 ( 1 − t ) β − 1 d t {\displaystyle F(x)=I_{x}(\alpha ,\beta )={\frac {\mathrm {B} _{x}(\alpha ,\beta )}{\mathrm {B} (\alpha ,\beta )}}={\frac {\int _{0}^{x}t^{\alpha -1}(1-t)^{\beta -1}dt}{\int _{0}^{1}t^{\alpha -1}(1-t)^{\beta -1}dt}}} .

Caratteristiche

I momenti semplici di una variabile aleatoria X {\displaystyle X} con distribuzione Beta di parametri ( α , β ) {\displaystyle (\alpha ,\beta )} sono

μ k = E [ X k ] = ∫ 0 1 x α + k − 1 ( 1 − x ) β − 1 d x ∫ 0 1 x α − 1 ( 1 − x ) β − 1 d x = B ( α + k , β ) B ( α , β ) = ( α ) k ( α + β ) k {\displaystyle \mu _{k}=E[X^{k}]={\frac {\int _{0}^{1}x^{\alpha +k-1}(1-x)^{\beta -1}dx}{\int _{0}^{1}x^{\alpha -1}(1-x)^{\beta -1}dx}}={\frac {\mathrm {B} (\alpha +k,\beta )}{\mathrm {B} (\alpha ,\beta )}}={\frac {(\alpha )_{k}}{(\alpha +\beta )_{k}}}} ,

dove x k {\displaystyle x_{k}} indica il fattoriale crescente con k fattori, ( x ) k = x ( x + 1 ) ⋯ ( x + k − 1 ) {\displaystyle (x)_{k}=x(x+1)\cdots (x+k-1)} . (L'ultima uguaglianza può essere dedotta dall'espressione della funzione Beta attraverso la funzione Gamma, B ( α , β ) = Γ ( α ) Γ ( β ) / Γ ( α + β ) {\displaystyle \mathrm {B} (\alpha ,\beta )=\Gamma (\alpha )\Gamma (\beta )/\Gamma (\alpha +\beta )} e dalla proprietà Γ ( x + 1 ) = x Γ ( x ) {\displaystyle \Gamma (x+1)=x\Gamma (x)} .)

I momenti semplici soddisfano quindi la relazione ricorsiva

μ k + 1 = α + k α + β + k μ k {\displaystyle \mu _{k+1}={\frac {\alpha +k}{\alpha +\beta +k}}\mu _{k}} .

In particolare, la distribuzione ha:

  • valore atteso E [ X ] = α α + β {\displaystyle E[X]={\frac {\alpha }{\alpha +\beta }}} ;
  • varianza Var ( X ) = α β ( α + β ) 2 ( α + β + 1 ) {\displaystyle {\text{Var}}(X)={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}} ;
  • indice di asimmetria γ 1 = 2 β − α α + β + 2 α + β + 1 α β {\displaystyle \gamma _{1}=2{\frac {\beta -\alpha }{\alpha +\beta +2}}{\sqrt {\frac {\alpha +\beta +1}{\alpha \beta }}}} ;
  • indice di curtosi γ 2 = 6 α 3 − 2 α 2 β − 2 α β 2 + β 3 + α 2 − 4 α β + β 2 α β ( α + β + 2 ) ( α + β + 3 ) {\displaystyle \gamma _{2}=6{\frac {\alpha ^{3}-2\alpha ^{2}\beta -2\alpha \beta ^{2}+\beta ^{3}+\alpha ^{2}-4\alpha \beta +\beta ^{2}}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}} .

Invertendo le relazioni qui sopra, che forniscono il valore atteso e la varianza in funzione dei parametri α {\displaystyle \alpha } e β {\displaystyle \beta } , possiamo esprimere univocamente i suddetti parametri in termini del valore atteso e della varianza:

α = E [ X ] ( E [ X ] ( 1 − E [ X ] ) Var ( X ) − 1 ) {\displaystyle \alpha =E[X]\left({\frac {E[X](1-E[X])}{{\text{Var}}(X)}}-1\right)} ;
β = ( 1 − E [ X ] ) ( E [ X ] ( 1 − E [ X ] ) Var ( X ) − 1 ) {\displaystyle \beta =(1-E[X])\left({\frac {E[X](1-E[X])}{{\text{Var}}(X)}}-1\right)} .

Queste formule vengono applicate nel metodo dei momenti, con la media e la varianza osservate su un campione.

L'entropia è

H ( X ) = log ⁡ B ( α , β ) − ( α − 1 ) ϝ ( α ) − ( β − 1 ) ϝ ( β ) + ( α + β − 2 ) ϝ ( α + β ) {\displaystyle H(X)=\log \mathrm {B} (\alpha ,\beta )-(\alpha -1)\digamma (\alpha )-(\beta -1)\digamma (\beta )+(\alpha +\beta -2)\digamma (\alpha +\beta )} ,

dove ϝ {\displaystyle \digamma } è la funzione digamma.

La moda della distribuzione dipende dai segni di α − 1 {\displaystyle \alpha -1} e β − 1 {\displaystyle \beta -1} , ed è unica solo se almeno uno dei due è positivo:

se α > 1 {\displaystyle \alpha >1} e β > 1 {\displaystyle \beta >1} allora la moda è α − 1 α + β − 2 {\displaystyle {\frac {\alpha -1}{\alpha +\beta -2}}} ;
se α > 1 {\displaystyle \alpha >1} (o α = 1 {\displaystyle \alpha =1} ) e β < 1 {\displaystyle \beta <1} allora la moda è 1;
se β > 1 {\displaystyle \beta >1} (o β = 1 {\displaystyle \beta =1} ) e α < 1 {\displaystyle \alpha <1} allora la moda è 0.

(La funzione di densità di probabilità ha un asintoto in 0 se α < 1 {\displaystyle \alpha <1} , in 1 se β < 1 {\displaystyle \beta <1} .)

Relazioni con altre distribuzioni

Una distribuzione Beta può essere definita su un qualunque intervallo [ a , b ] {\displaystyle [a,b]} , costruendo una nuova variabile casuale Y = a + ( b − a ) X {\displaystyle Y=a+(b-a)X} .

Se X {\displaystyle X} segue la distribuzione Beta di parametri ( α , β ) {\displaystyle (\alpha ,\beta )} allora 1 − X {\displaystyle 1-X} segue la distribuzione Beta di parametri ( β , α ) {\displaystyle (\beta ,\alpha )} .

  • La distribuzione Beta di parametri ( 1 , 1 ) {\displaystyle (1,1)} corrisponde alla distribuzione continua uniforme U ( [ 0 , 1 ] ) {\displaystyle {\mathcal {U}}([0,1])} sull'intervallo unitario.
  • La distribuzione di Dirichlet è una generalizzazione della distribuzione Beta: essa descrive la distribuzione a posteriori dei parametri di una distribuzione multinomiale a posteriori, appunto, di un'osservazione. La distribuzione di Dirichlet con due parametri è esattamente la distribuzione Beta.
  • Per α = β = 3 2 {\displaystyle \alpha =\beta ={\tfrac {3}{2}}} la densità di probabilità del tipo Beta f ( x ) = x ( 1 − x ) {\displaystyle f(x)={\sqrt {x(1-x)}}} è, in termini geometrici, la metà superiore di una circonferenza: ( 2 f ( x ) ) 2 + ( 2 x − 1 ) 2 = 1 {\displaystyle (2f(x))^{2}+(2x-1)^{2}=1} , descrive un semicerchio. La variabile aleatoria Y = r ( 2 X − 1 ) {\displaystyle Y=r(2X-1)} segue una distribuzione di Wigner di parametro r.
  • Se X {\displaystyle X} e Y {\displaystyle Y} sono due variabili aleatorie indipendenti con distribuzioni Gamma di rispettivi parametri ( α , θ ) {\displaystyle (\alpha ,\theta )} e ( β , θ ) {\displaystyle (\beta ,\theta )} , allora la variabile aleatoria X X + Y {\displaystyle {\tfrac {X}{X+Y}}} segue la distribuzione Beta di parametri ( α , β ) {\displaystyle (\alpha ,\beta )} .
  • Se la variabile aleatoria X {\displaystyle X} segue la distribuzione Beta di parametri ( α , β ) {\displaystyle (\alpha ,\beta )} allora la variabile aleatoria T = X 1 − X {\displaystyle T={\tfrac {X}{1-X}}} è descritta dalla distribuzione Beta del secondo tipo, che ha funzione di densità di probabilità
f ( t ) = x α − 1 / ( 1 − x ) α + β B ( α , β ) {\displaystyle f(t)={\frac {x^{\alpha -1}/(1-x)^{\alpha +\beta }}{\mathrm {B} (\alpha ,\beta )}}}
  • La distribuzione di Wilks Λ ( p , m , n ) {\displaystyle \Lambda (p,m,n)} può essere interpretata come la distribuzione che governa il prodotto X 1 ⋯ X n {\displaystyle X_{1}\cdots X_{n}} di n variabili aleatorie indipendenti X 1 , . . . , X n {\displaystyle X_{1},...,X_{n}} con rispettivi parametri ( m + 1 − p 2 , p 2 ) , . . . , ( m + n − p 2 , p 2 ) {\displaystyle ({\tfrac {m+1-p}{2}},{\tfrac {p}{2}}),...,({\tfrac {m+n-p}{2}},{\tfrac {p}{2}})} .
  • Se Y {\displaystyle Y} è una variabile aleatoria con distribuzione di Kumaraswamy di parametri ( a , b ) {\displaystyle (a,b)} allora X = Y a {\displaystyle X=Y^{a}} segue la distribuzione Beta di parametri ( 1 , b ) {\displaystyle (1,b)} .

Inferenza bayesiana

La distribuzione Beta e il processo di Bernoulli

E' immediato dimostrare che, se X è distribuita come una v.c. binomiale con parametri n e π

f ( x | π ) = B i n o m ( x | n ; π ) {\displaystyle f(x|\pi )=Binom(x|n;\pi )}

e il parametro π è distribuito a priori come una v.c. Beta con i parametri a e b

g ( π ) = B e t a ( π | a ; b ) {\displaystyle g(\pi )=Beta(\pi |a;b)}

allora il parametro π è distribuito a posteriori, anch'esso, come una v.c. Beta, ma con parametri a+x e b+n-x

g ( π | x ) = B e t a ( π | a + x ; b + n − x ) {\displaystyle g(\pi |x)=Beta(\pi |a+x;b+n-x)}

Come detto in precedenza, qualora il parametro π sia distribuito a priori come una variabile casuale rettangolare nell'intervallo [0;1] (ovvero ipotizzando a priori tutti i possibili valori di π equiprobabili), e pertanto a=1 e b=1, allora la distribuzione a posteriori del parametro π è una Beta con parametri x+1 e n-x+1

g ( π | x ) = ( n + 1 ) ( n x ) π x ( 1 − π ) n − x {\displaystyle g(\pi |x)=(n+1){n \choose x}\pi ^{x}(1-\pi )^{n-x}}

essa ha come valore modale p

p = x n {\displaystyle p={\frac {x}{n}}} , che corrisponde alla stima usata in ambito frequentistico, mentre il valore atteso o media, è
p = x + 1 n + 2 {\displaystyle p={\frac {x+1}{n+2}}} , che per x<n/2 è maggiore del valore modale x n {\displaystyle {\frac {x}{n}}} . Il valore atteso minimizza lo scarto quadratico.

Infatti, la probabilità di ottenere α − 1 {\displaystyle \alpha -1} successi e β − 1 {\displaystyle \beta -1} fallimenti in un processo di Bernoulli di parametro p è ( α + β − 2 α − 1 ) p α − 1 ( 1 − p ) β − 1 {\displaystyle {\tbinom {\alpha +\beta -2}{\alpha -1}}p^{\alpha -1}(1-p)^{\beta -1}} , proporzionale alla densità f ( p ) {\displaystyle f(p)} della distribuzione Beta di parametri ( α , β ) {\displaystyle (\alpha ,\beta )} .

Pertanto, come detto sopra, se la variabile aleatoria S {\displaystyle S} segue una distribuzione binomiale B ( P , α + β − 2 ) {\displaystyle {\mathcal {B}}(P,\alpha +\beta -2)} con parametro aleatorio P distribuito a priori uniformemente sull'intervallo unitario [ 0 , 1 ] {\displaystyle [0,1]} , a posteriori dell'osservazione S = α − 1 {\displaystyle S=\alpha -1} il parametro P segue la distribuzione B ( α , β ) {\displaystyle \mathrm {B} (\alpha ,\beta )} .

Più in generale, se S {\displaystyle S} è una variabile aleatoria con distribuzione binomiale B ( P , n ) {\displaystyle {\mathcal {B}}(P,n)} e il parametro P segue a priori la distribuzione B ( α , β ) {\displaystyle \mathrm {B} (\alpha ,\beta )} , allora a posteriori dell'osservazione S = s {\displaystyle S=s} il parametro P segue la distribuzione B ( α + s , β + n − s ) {\displaystyle \mathrm {B} (\alpha +s,\beta +n-s)} .

Il caso della distribuzione uniforme a priori è un caso particolare di quest'ultimo, essendo B ( 1 , 1 ) = U ( 0 , 1 ) {\displaystyle \mathrm {B} (1,1)={\mathcal {U}}(0,1)} .

Priori coniugate e la v.c. binomiale negativa

Se X è distribuita come una v.c. binomiale negativa con parametri m e θ

f ( x | θ ) = B i n N e g ( x | m ; θ ) {\displaystyle f(x|\theta )=BinNeg(x|m;\theta )}

e il parametro θ è distribuito a priori come una v.c. Beta con i parametri a e b

g ( θ ) = B e t a ( θ | a ; b ) {\displaystyle g(\theta )=Beta(\theta |a;b)}

allora il parametro θ è distribuito a posteriori anch'esso come una v.c. Beta, ma con parametri a+m e b+x

g ( θ | x ) = B e t a ( θ | a + m ; b + x ) {\displaystyle g(\theta |x)=Beta(\theta |a+m;b+x)}

Qualora la distribuzione a priori sia una variabile casuale rettangolare nell'intervallo [0;1] (ovvero ipotizzando a priori tutti i possibili valori di θ equiprobabili), e pertanto a=1 e b=1, allora la distribuzione a posteriori è una Beta con parametri m+1 e x+1

che ha come valore modale t

t=m/(m+x)

Similmente, se la variabile aleatoria T {\displaystyle T} segue la distribuzione di Pascal N B ( P , n ) {\displaystyle {\mathcal {NB}}(P,n)} e P segue a priori la distribuzione B ( α , β ) {\displaystyle \mathrm {B} (\alpha ,\beta )} , allora a posteriori dell'osservazione T = t {\displaystyle T=t} il parametro P segue la distribuzione B ( α + n , β + t ) {\displaystyle \mathrm {B} (\alpha +n,\beta +t)} .

Voci correlate

Altri progetti

Altri progetti

  • Wikimedia Commons
  • Collabora a Wikimedia Commons Wikimedia Commons contiene immagini o altri file su Distribuzione Beta

Collegamenti esterni

  • (EN) Eric W. Weisstein, Distribuzione Beta, su MathWorld, Wolfram Research. Modifica su Wikidata
Controllo di autoritàGND (DE) 4144975-7
  Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica