Onda triangolare
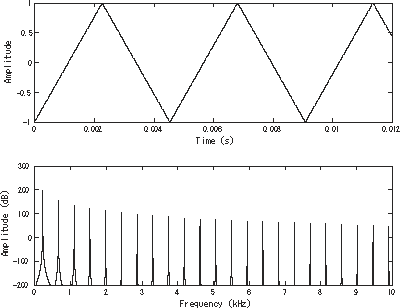
Un'onda triangolare è una forma d'onda non sinusoidale cosiddetta per l'aspetto dei suoi picchi, a forma di triangolo.
Analisi armonica
Come le onde quadre, l'onda triangolare contiene solo le armoniche dispari con la differenza che le armoniche più alte decadono molto più velocemente che nelle onde quadre, in modo proporzionale all'inverso del quadrato del numero di armonica mentre nell'onda quadra decadono rispetto all'inverso del numero di armonica.
È possibile approssimare un'onda triangolare con la sintesi additiva aggiungendo le armoniche pari della frequenza fondamentale, moltiplicando le armoniche poste in posizione (4n-1) per -1 (o cambiando la loro fase di π), e poi facendo decadere le armoniche per l'inverso del quadrato della loro frequenza relativa alla frequenza fondamentale.
La seguente serie di Fourier converge verso un'onda triangolare:
- dove è la frequenza angolare.

Un'altra definizione dell'onda triangolare, con ampiezza da -1 a 1 e periodo 2a è la seguente:
- dove rappresenta la funzione Floor di n.
Inoltre l'onda triangolare può essere data dal valore assoluto di un'onda a dente di sega:
L'onda triangolare può anche essere espressa come l'integrale dell'onda quadra:
Valore rms di un'onda triangolare alternata
In teoria dei segnali, il valore rms (root mean square o valore efficace) di un'onda triangolare alternata vale .
Si ponga infatti per (forma d'onda passante per l'origine). Dato che il grafico di è ancora periodico e sempre positivo, e in virtù della pendenza costante della curva tra 0 e , possiamo asserire
.
Generatore di onde triangolari
Un classico esempio di generatore di onde triangolari è un multivibratore astabile messo in serie con un integratore analogico, proprio per la suddetta caratteristica dell'onda triangolare, integrale dell'onda quadra.[1]
Note
- ^ Adel Sedra, K.C. Smith, Circuiti per la microelettronica, a cura di Aldo Ferrari, IV edizione, Roma, Edizioni Ingegneria 2000, pp. 1005, 1006, ISBN 88-86658-15-X.
Voci correlate

- Onda sinusoidale
- Onda a dente di sega
- Onda quadra
- Onda (fisica)
- Suono
Altri progetti
Altri progetti
- Wikimedia Commons
 Wikimedia Commons contiene immagini o altri file su Onda triangolare
Wikimedia Commons contiene immagini o altri file su Onda triangolare
Collegamenti esterni
- (EN) Eric W. Weisstein, Onda triangolare, su MathWorld, Wolfram Research.

 Portale Elettrotecnica
Portale Elettrotecnica Portale Fisica
Portale Fisica










![{\displaystyle V_{rms}={\sqrt {{\frac {1}{T}}\cdot \int _{-T/2}^{+T/2}V^{2}(t)dt}}={\sqrt {4\cdot {\frac {1}{T}}\cdot \int _{0}^{+T/4}\left({\frac {V_{0}\cdot t}{T/4}}\right)^{2}dt}}={\sqrt {{\frac {64V_{0}^{2}}{T^{3}}}\cdot \left[{\frac {t^{3}}{3}}\right]_{0}^{T/4}}}={\sqrt {{\frac {64V_{0}^{2}}{T^{3}}}\cdot {\frac {T^{3}}{3\cdot 64}}}}={\frac {V_{0}}{\sqrt {3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b98886ef9775fa943b85b363fd146f6144cd573c)











