楕円曲線暗号

楕円曲線暗号（だえんきょくせんあんごう、Elliptic Curve Cryptography、ECC）とは、楕円曲線上の離散対数問題 (EC-DLP) の困難性を安全性の根拠とする暗号。1985年頃にビクター・S・ミラー（英語版）とニール・コブリッツ（英語版）が各々発明した。

具体的な暗号方式の名前ではなく、楕円曲線を利用した暗号方式の総称である。DSAを楕円曲線上で定義した楕円曲線DSA (ECDSA)、ディフィー・ヘルマン鍵共有（DH鍵共有）を楕円化した楕円曲線ディフィー・ヘルマン鍵共有 (ECDH) などがある。公開鍵暗号が多い。

EC-DLPを解く準指数関数時間アルゴリズムがまだ見つかっていないため、それが見つかるまでの間は、RSA暗号などと比べて、同レベルの安全性をより短い鍵で実現でき、処理速度も速いことをメリットとして、ポストRSA暗号として注目されている。ただしP=NPが成立した場合、EC-DLPを多項式時間で解くアルゴリズムが存在するということになり、ECCの安全性は崩壊する（公開鍵暗号自体が崩壊）。また、送信者が暗号化時に適当な乱数（公開鍵とは違うモノ）を使うので鍵が同じでも平文と暗号文の関係が1対1でない点にも注意（ElGamal暗号でも同様）。

一部の楕円曲線には、DLPを解く多項式時間アルゴリズムが見つかっているため、注意が必要である。

歴史

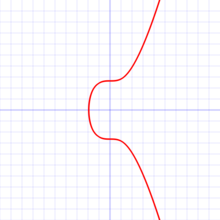
暗号理論に楕円曲線を利用しようというアイディアは、1985年にニール・コブリッツ[1] と ビクター・S・ミラー[2] によって独立に提案された。楕円曲線暗号は、2004～2005年ごろから広く使用されるようになっている。

理論

楕円曲線の例： secp256k1(後述)で規定されている R 2 {\displaystyle \mathbb {R} ^{2}} 上の y 2 = x 3 + 7 {\displaystyle y^{2}=x^{3}+7} のグラフ。

実平面 R 2 {\displaystyle \mathbb {R} ^{2}} 上の点を P ( x , y ) {\displaystyle P(x,y)} で表した場合、 R 2 {\displaystyle \mathbb {R} ^{2}} 上で定義される楕円曲線 E : y 2 = x 3 + a x + b {\displaystyle E:y^{2}=x^{3}+ax+b} (ワイエルシュトラスの標準形)では、 E {\displaystyle E} 上の点に接弦法(またはバシェ(Bachet)の方法)[3] と呼ばれる加法的な2項演算により加群の構造を与えることができる(零元は通常は無限遠点と定義される。これを O {\displaystyle O} で表す)。

楕円曲線暗号で扱う楕円曲線とは、 E {\displaystyle E} 上の有理点を、ある素数 p {\displaystyle p} で還元した有限体 F p {\displaystyle \mathbf {F} _{p}} 上の離散的楕円曲線 E ( F p ) {\displaystyle E(\mathbf {F} _{p})} であり、還元によって上記の加群の構造は E ( F p ) {\displaystyle E(\mathbf {F} _{p})} 上の加群の構造に写される。

楕円曲線上の加法

楕円曲線 E {\displaystyle E} 上の異なる2点を P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) {\displaystyle P_{1}\,(x_{1},\,y_{1}),\,P_{2}\,(x_{2},\,y_{2})} とする場合、その接弦法の加法を P 1 + P 2 {\displaystyle P_{1}+P_{2}} で表すことにすると、 P 3 ( x 3 , y 3 ) = P 1 + P 2 {\displaystyle P_{3}\,(x_{3},y_{3})=P_{1}+P_{2}} は次の式で計算される[4]。

まず、 P 1 + O = O + P 1 = P 1 {\displaystyle P_{1}+O=O+P_{1}=P_{1}} である。すなわち、無限遠点 O {\displaystyle O} が零元である。

もし x 1 = x 2 , y 1 = − y 2 {\displaystyle x_{1}=x_{2},y_{1}=-y_{2}} ならば、 P 1 + P 2 = O {\displaystyle P_{1}+P_{2}=O} である。

それ以外の場合、 P 3 = P 1 + P 2 {\displaystyle P_{3}=P_{1}+P_{2}} は、2点 P 1 , P 2 {\displaystyle P_{1},\,P_{2}} を通る直線と E {\displaystyle E} との（ P 1 {\displaystyle P_{1}} および P 2 {\displaystyle P_{2}} と異なる）交点の、y座標の符号を反転したものである。すなわち P 3 ( x 3 , y 3 ) {\displaystyle P_{3}\,(x_{3},\,y_{3})} は以下のようになる。

x 3 = ϕ 2 − x 1 − x 2 , {\displaystyle x_{3}=\phi ^{2}-x_{1}-x_{2},}
y 3 = − ϕ x 3 − ψ . {\displaystyle y_{3}=-\phi x_{3}-\psi .}
ただし ϕ , ψ {\displaystyle \phi ,\,\psi } は
ϕ = y 2 − y 1 x 2 − x 1 , {\displaystyle \phi ={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}},}
ψ = y 1 x 2 − y 2 x 1 x 2 − x 1 . {\displaystyle \psi ={\frac {y_{1}x_{2}-y_{2}x_{1}}{x_{2}-x_{1}}}.}

上の方法で定義された2項演算は加法として必要な次の性質を備えている。

  • 零元 O {\displaystyle O} の存在
  • 各元 P 1 {\displaystyle P_{1}} に対する逆元 − P 1 {\displaystyle -P_{1}} の存在
  • 可換性： P 1 + P 2 = P 2 + P 1 {\displaystyle P_{1}+P_{2}=P_{2}+P_{1}} (定義式の対称性から明らか)
  • 結合性： ( P 1 + P 2 ) + P 3 = P 1 + ( P 2 + P 3 ) {\displaystyle (P_{1}+P_{2})+P_{3}=P_{1}+(P_{2}+P_{3})} (煩雑であるが定義式を丁寧に解けば証明できる)

楕円曲線上での2倍算

楕円曲線 E {\displaystyle E} 上の点 P 1 ( x 1 , y 1 ) {\displaystyle P_{1}\,(x_{1},\,y_{1})} に対し、さらに P 1 {\displaystyle P_{1}} を加算する場合、つまり P 1 + P 1 = 2 P 1 {\displaystyle P_{1}+P_{1}=2P_{1}} を求める場合、上記の方法は使えない。

この場合、まず y 1 = 0 {\displaystyle y_{1}=0} のときは、 2 P A = O {\displaystyle 2P_{\!A}=O} である。また、 2 O = O + O = O {\displaystyle 2O=O+O=O} である。

それ以外の場合は、 P 4 = 2 P 1 {\displaystyle P_{4}=2P_{1}} は、 P 1 {\displaystyle P_{1}} での E {\displaystyle E} の接線が E {\displaystyle E} 自身と交わる（ P 1 {\displaystyle P_{1}} とは異なる）交点の、 y {\displaystyle y} 座標の符号を反転したものである。すなわち P 4 ( x 4 , y 4 ) {\displaystyle P_{4}\,(x_{4},\,y_{4})} は以下で求められる。

x 4 = ϕ 2 − 2 x 1 , {\displaystyle x_{4}=\phi ^{2}-2x_{1},}
y 4 = − ϕ x 4 − ψ . {\displaystyle y_{4}=-\phi x_{4}-\psi .}
この式は異なる二点の加算の場合と同じであるが、 ϕ , ψ {\displaystyle \phi ,\,\psi } の計算式が次のように変わる。
ϕ = 3 x 1 2 + a 2 y 1 , {\displaystyle \phi ={\frac {3x_{1}^{2}+a}{2y_{1}}},}
ψ = − 3 x 1 3 − a x 1 + 2 y 1 2 2 y 1 . {\displaystyle \psi ={\frac {-3x_{1}^{3}-ax_{1}+2y_{1}^{2}}{2y_{1}}}.}

スカラー倍算

スカラー倍算（Scalar Multiplication）は楕円曲線上における掛け算である。楕円曲線上の点と点を掛けるのではなく、点に整数（スカラー）を掛けることに注意。

E {\displaystyle E} 上のある点 P 1 {\displaystyle P_{1}} を始点として、これに順次 P 1 {\displaystyle P_{1}} 自身を n − 1 {\displaystyle n-1} 回加算して得られる点を n P 1 {\displaystyle nP_{1}} で表すことにする。この操作は O {\displaystyle O} に P 1 {\displaystyle P_{1}} を n {\displaystyle n} 回加算することと同じである。 O {\displaystyle O} に − P 1 {\displaystyle -P_{1}} を n {\displaystyle n} 回加算すれば − n P 1 {\displaystyle -nP_{1}} が得られる。 このようにして、 E {\displaystyle E} 上の点と整数の掛け算が定義できる。この操作をスカラー倍算（Scalar Multiplication）と呼ぶことにする。

P 1 {\displaystyle P_{1}} を始点として、加法により生成される点列(つまり全ての整数についての P 1 {\displaystyle P_{1}} のスカラー倍算の集合)は、 E {\displaystyle E} 上の巡回加群を作っている(これを ⟨ P 1 ⟩ {\displaystyle \langle P_{1}\rangle } と表すことにする)。

楕円曲線上の有理点

楕円曲線のパラメーター a , b {\displaystyle a,b} が有理数の場合、2つの有理点( x , y {\displaystyle x,y} が共に有理数の点)を加算して得られる点はやはり有理点である。つまり、 E {\displaystyle E} 上の全ての有理点の集合＋無限遠点 O {\displaystyle O} を E ( Q ) {\displaystyle E(\mathbb {Q} )} と表すと、 E ( Q ) {\displaystyle E(\mathbb {Q} )} は加法について E {\displaystyle E} の部分加群を成している。また、 E ( Q ) {\displaystyle E(\mathbb {Q} )} 上のある有理点を始点として加法により生成される E ( Q ) {\displaystyle E(\mathbb {Q} )} 上の点列は、 E ( Q ) {\displaystyle E(\mathbb {Q} )} 上の全ての点が成す加群の部分加群(巡回群)を成している。さらに始点が整点( x , y {\displaystyle x,y} が共に整数の点)でない場合、この巡回加群の位数は無限大である(Nagell-Lutzの定理[5])。

また、 E ( Q ) {\displaystyle E(\mathbb {Q} )} 全体が成す加群は、有限個の始点が生成する巡回群の直和になることが知られている(モーデルの定理)。

素数 p による還元

楕円曲線暗号で扱う楕円曲線とは、 E ( Q ) {\displaystyle E(\mathbb {Q} )} をある素数 p {\displaystyle p} で還元した有限体 F p {\displaystyle \mathbf {F} _{p}} 上の離散的楕円曲線であり、これを E ( F p ) {\displaystyle E(\mathbf {F} _{p})} と表すことにする(無限遠点 O {\displaystyle O} も含む)。ここで素数 p {\displaystyle p} による還元とは、有理数体 Q {\displaystyle \mathbb {Q} } から有限体 F p {\displaystyle \mathbf {F} _{p}} 上への次の写像 f p {\displaystyle f_{p}} を作用させることである[6]。

有理数を u / v {\displaystyle u/v} (uは整数、vは自然数)と表した場合、

f p ( u / v ) = ( u mod p ) ( v mod p ) − 1 mod p {\displaystyle f_{p}(u/v)=(u{\bmod {\,}}p)(v{\bmod {\,}}p)^{-1}{\bmod {\,}}p}
ただし、 ( v mod p ) − 1 {\displaystyle (v{\bmod {\,}}p)^{-1}} は F p {\displaystyle \mathbf {F} _{p}} の元 v mod p {\displaystyle v{\bmod {\,}}p} の F p {\displaystyle \mathbf {F} _{p}} における逆元とする。

f p {\displaystyle f_{p}} は有理数体 Q {\displaystyle \mathbb {Q} } から 有限体 F p {\displaystyle \mathbf {F} _{p}} への体準同型写像であり、 Q {\displaystyle \mathbb {Q} } 上の加法、乗法、逆元は F p {\displaystyle \mathbf {F} _{p}} 上の加法、乗法、逆元に写される。例えば Q {\displaystyle \mathbb {Q} } における除算は、 F p {\displaystyle \mathbf {F} _{p}} では逆元を乗ずる操作に写される。

上述の接弦法の加法の計算式は、 x 2 − x 1 {\displaystyle x_{2}-x_{1}} または y 1 {\displaystyle y_{1}} による除法を、 F p {\displaystyle \mathbf {F} _{p}} における逆元 ( x 2 − x 1 ) − 1 {\displaystyle (x_{2}-x_{1})^{-1}} または y 1 − 1 {\displaystyle y_{1}^{-1}} による乗法に置き換えればそのまま成り立つ。

なお、前述のように、 Q {\displaystyle \mathbb {Q} } 上においては、始点が整点でない巡回加群の位数は無限大であるが、楕円曲線 E {\displaystyle E} の f p {\displaystyle f_{p}} による像である F p {\displaystyle \mathbf {F} _{p}} 上の楕円曲線 E ( F p ) {\displaystyle E(\mathbf {F} _{p})} は有限集合であり、当然位数も有限となる。

補足：上記の方法を拡張して、有限体 F p {\displaystyle \mathbf {F} _{p}} の m {\displaystyle m} 次拡大体 F p m {\displaystyle \mathbf {F} _{p^{m}}} 上での楕円曲線 E ( F p m ) {\displaystyle E(\mathbf {F} _{p^{m}})} を用いる暗号法も考案されており、実用的な仕様も公開されているが、話が煩雑になるので立ち入らないことにする。

離散対数と離散対数問題

楕円曲線 E ( F p ) {\displaystyle E(\mathbf {F} _{p})} 上のある点 G {\displaystyle G} から、 2 G , 3 G , 4 G , … {\displaystyle 2G,3G,4G,\ldots } を計算していくと、次々と異なる（楕円曲線上の）点が得られるが、上述のように E ( F p ) {\displaystyle E(\mathbf {F} _{p})} は有限集合であるから、この点列はいずれは無限遠点 n G = O {\displaystyle nG=O} に到達する（ただし楕円曲線によってはそのようなGはG=Oしか無い事もある）。その後は、 ( n + 1 ) G = G , ( n + 2 ) G = 2 G , ( n + 3 ) G = 3 G , … {\displaystyle (n+1)G=G,(n+2)G=2G,(n+3)G=3G,\ldots } と繰り返される。このように G {\displaystyle G} からスカラー倍算によって得られる点の集合を ⟨ G ⟩ = { G , 2 G , 3 G , … , O } {\displaystyle \langle G\rangle =\{G,2G,3G,\ldots ,O\}} と書くことにすると、 ⟨ G ⟩ {\displaystyle \langle G\rangle } は巡回群となる。巡回群の位数は n {\displaystyle n} であり、 ⟨ G ⟩ {\displaystyle \langle G\rangle } を生成する元 G {\displaystyle G} はベースポイントとも呼ばれる。

E ( F p ) {\displaystyle E(\mathbf {F} _{p})} 上の全点数は高々 2 p + 1 {\displaystyle 2p+1} (無限遠点 O {\displaystyle O} を含む)であり、位数 n {\displaystyle n} はこれより小さくなるが[7]、楕円曲線のパラメーター a , b , p {\displaystyle a,b,p} に依存し、実際の値はSchoofのアルゴリズムまたはその改良版などを用いて n {\displaystyle n} を計算しないと分からない( n {\displaystyle n} の存在範囲については、ハッセの定理という手掛かりがある)。 n {\displaystyle n} が素数の場合、巡回群 ⟨ G ⟩ {\displaystyle \langle G\rangle } の全ての元は ⟨ G ⟩ {\displaystyle \langle G\rangle } の生成元であり、位数は n {\displaystyle n} になる。

楕円曲線暗号においては n {\displaystyle n} はなるべく大きな素数であることが、暗号強度を強くする上で必要とされるが、これに適したパラメーター a , b , p {\displaystyle a,b,p} の決定は、多数のパラメーターの候補について、Schoofのアルゴリズムまたはその改良版などを用いて n {\displaystyle n} を計算するという試行錯誤により行われる[8]。

巡回群 ⟨ G ⟩ {\displaystyle \langle G\rangle } の任意の要素（楕円曲線上の点） X {\displaystyle X} に対し、 X = a G {\displaystyle X=aG} を満たす a {\displaystyle a} が { 0 , 1 , … , n − 1 } {\displaystyle \{0,1,\ldots ,n-1\}} の中に常にただ一つ存在する。このような a {\displaystyle a} を X {\displaystyle X} の離散対数と呼ぶ。また、 ⟨ G ⟩ {\displaystyle \langle G\rangle } から無作為に選らばれた X {\displaystyle X} を与えられ、その離散対数を求めよという問題を、楕円曲線上の離散対数問題 と呼ぶ。

また、 ⟨ G ⟩ {\displaystyle \langle G\rangle } から無作為に選ばれた二つの点 X = a G , Y = b G {\displaystyle X=aG,Y=bG} を与えられ、 a b G {\displaystyle abG} を求めよという問題を、楕円曲線上のディフィー・ヘルマン問題 と呼ぶ。

最もポピュラーな離散対数問題は、 p , g {\displaystyle p,g} と y = g x mod p {\displaystyle y=g^{x}{\bmod {p}}} から x {\displaystyle x} を求めよ、という問題であり、 g ∈ Z p ∗ ( = Z / p Z ) × {\displaystyle g\in Z_{p}^{*}(=Z/pZ)^{\times }} から生成される乗法群の上で定義されている。これに対して、楕円曲線は加法群であるため、 Y = a P {\displaystyle Y=aP} を満たす a {\displaystyle a} を離散対数と呼ぶ。

巡回群の位数 n {\displaystyle n} が小さければ、離散対数問題やディフィー・ヘルマン問題が容易に解けてしまうため、位数が巨大な素数になるようなベースポイント（と楕円曲線）が使用される。

楕円曲線のパラメーターの一例として、ビットコインで使われている楕円曲線暗号である secp256k1 のものを示す[9]。

p = 2 256 − 2 32 − 2 9 − 2 8 − 2 7 − 2 6 − 2 4 − 1 {\displaystyle p=2^{256}-2^{32}-2^{9}-2^{8}-2^{7}-2^{6}-2^{4}-1}
{\displaystyle \,} = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
E : y 2 = x 3 + 7 {\displaystyle E:\,y^{2}=x^{3}+7}
G = ( x G , y G ) {\displaystyle G=(x_{G},y_{G})}
x G {\displaystyle x_{G}} = 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
y G {\displaystyle y_{G}} = 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
n {\displaystyle n} = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

スカラー倍算の効率化

暗号化・復号の過程において、 Q = d P {\displaystyle Q=dP} （ P , Q {\displaystyle P,\,Q} は楕円曲線上の点）というスカラー倍算を行う。 ナイーヴな実装としては Q = ( ⋯ ( ( P + P ) + P ) + ⋯ ) + P {\displaystyle Q=(\cdots ((P+P)+P)+\cdots )+P} というように Pを ( d − 1 ) {\displaystyle (d-1)} 回加算（1回目は2倍算となる）するが、これでは効率が悪い。

スカラー倍算はRSA暗号などにおけるべき乗剰余演算とリンクしており、これの高速化手法もそれから流用できるものが多い。例えば、そのひとつとして有名なBinary法では、dを2進数表記し、dの各ビット d i {\displaystyle d_{i}} が "0" の場合は2倍算のみを行い、"1" の場合は2倍算と加算を行うことにより、ナイーブな実装と同じ計算をより高速に行なっている。この計算手法では、2倍算はべき乗剰余演算における自乗算、加算は掛け算にそれぞれ対応している。

この演算は楕円曲線暗号の根幹を成している部分であり、楕円曲線暗号を利用する際の時間の大半を占めている。ゆえに、ICカードなどハードウェア上に演算回路を実装する場合はサイドチャネル攻撃（特にSPA、DPA）のターゲットとなる箇所なので工夫が必要となる。

攻撃手法

サイドチャネル攻撃

楕円曲線上で楕円加算 P + Q を行う場合、加算(P ≠ Q)と2倍算(P = Q)では演算プロセスが大きく異なる。そのため、サイドチャネル攻撃（例えば、タイミング攻撃や単純電力解析/差分電力解析）への対策（例えば [10] など）が必要である。あるいは、ツイステッドエドワーズ曲線（英語版）を使うこともできる。この曲線は、加算と2倍算を同じ演算プロセスで実行できる特別な楕円曲線の族である。[11]

量子コンピュータを用いた攻撃

離散対数問題を効率的に解くことのできるショアのアルゴリズムは、楕円曲線暗号の解読にも利用できる。256ビットの法を持つ楕円曲線暗号（128ビット安全）を破るためには、2330量子ビット、1,260億トフォリゲートのリソースを持つ量子コンピュータが必要であると見積もられている。[12] 一方、アメリカ国立標準技術研究所の勧告（NIST SP 800-57）によりこれと同等のセキュリティレベルとされる3072ビット鍵のRSA暗号を破るためには、6146量子ビット、18.6兆トフォリゲートが必要であり[12]、量子コンピュータにとっては、RSA暗号に比べ楕円曲線暗号は攻撃しやすいといえる。[独自研究?]いずれにせよ、これらのリソースは現在実存する量子コンピュータのリソースをはるかに超えており、このようなコンピュータの構築は10年以上先になると見られている[要出典]。

同種写像暗号は、楕円曲線の同種写像を用いた暗号方式であり、量子コンピュータに対して耐性がある（耐量子）と考えられている。同種写像暗号の例としてディフィー・ヘルマン鍵共有と同様に鍵共有を行うSIDHがある。従来の楕円曲線暗号と同じ体の演算を多く使用し、必要な計算量や通信量は現在使用されている多くの公開鍵システムと同程度である。 [13]

解読

脚注

  1. ^ Koblitz, N. (1987). “Elliptic curve cryptosystems”. Mathematics of Computation 48 (177): 203?209. doi:10.2307/2007884. JSTOR 2007884. 
  2. ^ Miller, V. (1985). “Use of elliptic curves in cryptography”. CRYPTO. Lecture Notes in Computer Science 85: 417?426. doi:10.1007/3-540-39799-X_31. ISBN 978-3-540-16463-0. 
  3. ^ 足立恒雄『フェルマーの大定理 [第3版]』日本評論社、1996年5月、164-167頁。ISBN 4-535-78231-8。 
  4. ^ J.Song『プログラミング・ビットコイン ゼロからビットコインをプログラムする方法』中川卓俊、住田和則、中村昭雄 監訳 星野靖子 訳、オライリー・ジャパン (オーム社)、2020年10月、36-40頁。ISBN 978-4-87311-902-1。 
  5. ^ J.H.シルヴァーマン、J.テイト『楕円曲線論入門』足立恒雄ほか 訳、丸善出版、2012年7月、61頁。ISBN 978-4-621-06571-6。 
  6. ^ コブリッツ 1997, pp. 256, 272.
  7. ^ コブリッツ 1997, p. 246.
  8. ^ コブリッツ 1997, pp. 253–261.
  9. ^ S.Chandrashekar & N.Ramani (27 January 2010). SEC 2：Recommended Elliptic Curve Domain Parameters (Version 2.0) (PDF) (Report). Standards for Efficient Cryptography Group (SECG). p. 13. 2024年5月30日閲覧。
  10. ^ Hedabou, M.; Pinel, P.; Beneteau, L. (2004). “A comb method to render ECC resistant against Side Channel Attacks”. IACR ePrint Report. http://eprint.iacr.org/2004/342. 
  11. ^ “Cr.yp.to: 2014.03.23: How to design an elliptic-curve signature system”. 2020年1月2日閲覧。
  12. ^ a b Roetteler, Martin; Naehrig, Michael; Svore, Krysta M.; Lauter, Kristin (2017). "Quantum resource estimates for computing elliptic curve discrete logarithms". arXiv:1706.06752 [quant-ph]。
  13. ^ De Feo, Luca; Jao, David; Plut, Jerome (2014). “Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies”. Journal of Math. Cryptology: 209–247. https://www.degruyter.com/view/j/jmc.2014.8.issue-3/jmc-2012-0015/jmc-2012-0015.xml. 

参考文献

  • N.コブリッツ『数論アルゴリズムと楕円暗号理論入門』櫻井幸一 訳、シュプリンガー・フェアラーク東京、1997年8月。ISBN 4-431-70727-1。 
  • Blake; Seroussi; Smart (1999). Elliptic Curves in Cryptography. CAMBRIDGE UNIVERSITY PRESS 

関連項目