Multiplicadores de Lagrange

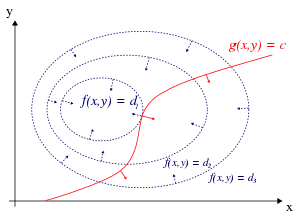
Em matemática, em problemas de otimização, o método dos multiplicadores de Lagrange permite encontrar extremos (máximos e mínimos) de uma função de uma ou mais variáveis suscetíveis a uma ou mais restrições.^[2]

Por exemplo (veja a figura 1 à direita), considere o problema de otimização

maximize ${\displaystyle f(x,y),}$ ou seja, deseja-se encontrar o ponto máximo desta função

sujeito a ${\displaystyle g(x,y)=c.}$

O método consiste em introduzir uma variável nova (${\displaystyle \lambda ,}$ normalmente), chamada de multiplicador de Lagrange. A partir disso, estuda-se a função de Lagrange, assim definida:

${\displaystyle \Lambda (x,y,\lambda )=f(x,y)-\lambda \cdot {\Big (}g(x,y)-c{\Big )},}$

Nesta função, o termo ${\displaystyle \lambda }$ pode ser adicionado ou subtraído. Se ${\displaystyle f(x,y)}$ é um ponto de máximo para o problema original, então existe um ${\displaystyle \lambda }$ tal que ${\displaystyle (x,y,\lambda )}$ é um ponto estacionário para a função lagrangiana, ou seja, existe um ponto para o qual as derivadas parciais de ${\displaystyle \Lambda }$ são iguais a zero.

No entanto, nem todos os pontos estacionários permitem uma solução para o problema original. Portanto, o método dos multiplicadores de Lagrange garante uma condição necessária para a otimização em problemas de otimização com restrição.^{[3][4][5][6][7]}

O nome "multiplicador de Lagrange" é uma homenagem a Joseph Louis Lagrange.

Definição

Considere uma função de ${\displaystyle n}$ variáveis ${\displaystyle f(x_{1},x_{2},...,x_{n})\quad }$e ${\displaystyle m}$ funções de restrição ${\displaystyle g_{1}(x_{1},x_{2},...,x_{n})\quad ...\quad g_{m}(x_{1},x_{2},...,x_{n})}$. Sejam estas funções deriváveis em primeira ordem com derivadas contínuas e que para qualquer ponto do domínio existe algum ${\displaystyle i}$ para o qual ${\displaystyle \nabla g_{i}(x)\neq 0}$, se ${\displaystyle f}$ tiver um extremo relativo dentro de suas restrições, este ponto ocorre em um ponto ${\displaystyle P(x_{1}^{*},x_{2}^{*},...,x_{n}^{*}),}$ tal que ${\displaystyle P}$ pertença a uma superfície de restrição de ${\displaystyle f}$ na qual a seguinte condição seja satisfeita:

${\displaystyle \nabla f(x_{1}^{*},x_{2}^{*},...,x_{n}^{*})=\sum _{i=1}^{m}\lambda _{i}\nabla g_{i}(x_{1}^{*},x_{2}^{*},...,x_{n}^{*})}$^[1]

${\displaystyle \lambda =(\lambda _{1},\lambda _{2},\ldots \,\lambda _{m})}$ são os multiplicadores de Lagrange.

A solução recai em resolver um sistema com ${\displaystyle n+m}$ equações (as ${\displaystyle n}$ equações obtidas pela diferenciação, e as ${\displaystyle m}$ restrições ${\displaystyle g_{i}}$) e ${\displaystyle n+m}$ incógnitas (a coordenada de ${\displaystyle P}$ no espaço de ${\displaystyle n}$ dimensões e os ${\displaystyle m}$ multiplicadores de Lagrange).

Utilização

O método de lagrange é empregado na resolução de problemas de Programação, é uma ferramenta importante em restrições de igualdade.

Exemplo

A função potencial gravitacional em relação a um corpo celeste: ${\displaystyle P(x,y,z)={\frac {-GM}{r}}}$ , onde ${\displaystyle r=[(x-x_{i})^{2}+(y-y_{i})^{2}+(z-z_{i})^{2}]^{\frac {1}{2}}}$ e ${\displaystyle (x_{i},y_{i},z_{i})}$ são as coordenadas do centro do corpo celeste.

O problema é: a uma dada distância da Terra e da Lua, ou seja, fixando-se os potenciais gravitacionais relativos a esses 2 corpos, deseja-se saber qual o ponto em que a energia potencial gravitacional gerada pela massa do Sol é máxima (ou mínima).

A figura abaixo mostra a situação, onde os centros dos 3 corpos estão no plano da tela, As superfícies esféricas equipotenciais da Terra e da Lua aparecem como círculos no plano da tela. Sua intercessão é um círculo num plano normal à tela, que a cruza nos pontos ${\displaystyle A}$ e ${\displaystyle B}$. Esses pontos são a solução do problema, pois um é o mais próximo e o outro é o mais distante do Sol, entre todo o conjunto de pontos desse círculo de intercessão das superfícies.

Qual a relação com os multiplicadores de Lagrange? Basta lembrar que a aceleração da gravidade é o gradiente do potencial gravitacional, e ela aponta para os centros dos corpos. Em geral, ao longo do círculo normal à tela, de intercessão entre as superfícies potenciais da Terra e Lua, esses vetores dirigidos respectivamente para o centro do Sol, da Terra e da Lua são linearmente independentes. Mas nos pontos ${\displaystyle A}$ e ${\displaystyle B}$ eles estão no mesmo plano, e um deles pode ser escrito como uma combinação linear dos outros.

Portanto pode-se escrever: ${\displaystyle a_{s}=\lambda _{1}a_{t}+\lambda _{2}a_{l}}$ ou

                     ${\displaystyle \nabla P_{s}(x,y,z)=\sum _{i=1}^{2}\lambda _{i}\nabla g_{i}(x,y,z)}$

onde: ${\displaystyle g_{1}=P_{t}(x,y,z)-C_{1}}$ e ${\displaystyle g_{2}=P_{l}(x,y,z)-C_{2}}$

${\displaystyle P_{s}(x,y,z)}$ é o potencial gravitacional do Sol, ${\displaystyle P_{t}(x,y,z)}$ é o da Terra e ${\displaystyle P_{l}(z,y,z)}$ é o da Lua. Como a restrição são as superfícies equipotenciais, as funções ${\displaystyle g_{i}}$ são zero para os pontos em que os potenciais são ${\displaystyle C_{1}}$ e ${\displaystyle C_{2}}$ respectivamente.^[8]

Ver também

• Gradiente

Referências

Ligações externas

• http://fma.if.usp.br/~fleming/lagrange/node4.html  Em falta ou vazio |título= (ajuda)
• Texto sobre multiplicadores de lagrange com exemplos como encontrar ${\displaystyle \lambda :}$

Este artigo sobre matemática é um esboço. Você pode ajudar a Wikipédia expandindo-o. v d e