Prímtényező

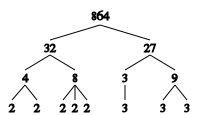
A számelméletben egy pozitív egész szám prímtényezőin vagy törzstényezőin a szám prímszám osztóinak összességét értjük.^[1] Egy pozitív egész szám prímfelbontása: a szám prímtényezőinek listázása, annak figyelembevételével, hogy hányszor szerepelnek a szám osztói között. A számelmélet alaptétele kimondja, hogy minden pozitív egész szám egyféleképpen bontható fel prímtényezők szorzatára.^[2]

A prímtényezős felbontást a rövidség érdekében hatványformában szokás felírni. Például

${\displaystyle 360=2\times 2\times 2\times 3\times 3\times 5=2^{3}\times 3^{2}\times 5,}$

melyben a 2, 3 és 5 prímtényezők multiplicitása 3, 2 illetve 1.

A ${\displaystyle n=\prod p_{i}^{\alpha _{i}}}$ felbontást a szám kanonikus alakjának is nevezik (pl. ${\displaystyle 12=2^{2}\cdot 3}$).

Egy n szám p prímtényezőjét tekintve p multiplicitása az a legnagyobb a kitevő, amire p^a osztója n-nek.

Egy n pozitív egész számra a prímtényezők száma és a prímtényezők összege (a multiplicitást nem tekintve) olyan számelméleti függvények, melyek additívak, de nem totálisan additívak.^[3]

Négyzetszámok

A négyzetszámok arról ismerhetőek meg, hogy minden prímtényezőjük páros multiplicitással rendelkezik. Például a 144 (a 12 négyzete) prímtényezői:

${\displaystyle 144=2\times 2\times 2\times 2\times 3\times 3=2^{4}\times 3^{2}.}$

Ezeket átrendezve:

${\displaystyle 144=2\times 2\times 2\times 2\times 3\times 3=(2\times 2\times 3)\times (2\times 2\times 3)=(2\times 2\times 3)^{2}=(12)^{2}.}$

Mivel minden prímtényező páros számúszor jelenik meg, az eredeti szám kifejezhető valamely kisebb szám négyzeteként. Hasonlóan, a köbszámok prímtényezőinek multiplicitása a 3 többszöröse s.í.t.

Relatív prímek

A közös prímtényezővel nem rendelkező pozitív egész számokat relatív prímeknek (angolul: coprime) nevezik. Ha a és b pozitív egész számok relatív prímek, ha legnagyobb közös osztójuk lnko(a, b) = 1. Az euklideszi algoritmussal meghatározható, hogy két szám relatív prím-e prímtényezőik ismerete nélkül is; az algoritmus a számjegyek száma szerint polinomiális időben fut le.

Az 1 szám minden pozitív egésszel és önmagával is relatív prím. Ennek oka, hogy nincsenek prímtényezői, ő az üres szorzat. Tehát lnko(1, b) = 1 bármely b ≥ 1.

Kriptográfiai alkalmazásai

A számok prímfelbontása titkosítási rendszerek kriptográfiai biztonságának fontos részét képezi;^[4] a probléma ismereteink szerint a polinomiálisnál hosszabb időt vesz igénybe; viszonylag könnyű olyan problémát megalkotni, aminek megoldása az univerzum életkoránál hosszabb időt venne igénybe jelenlegi algoritmusainkkal.

Omega-függvények

Az ω(n) (omega) megmutatja az n szám különböző prímtényezőinek számát, míg a Ω(n) (nagy omega) függvény, az n szám összes prímtényezőjének a számát^[2] Ha

${\displaystyle n=\prod _{i=1}^{\omega (n)}p_{i}^{\alpha _{i}}}$,

akkor

${\displaystyle \Omega (n)=\sum _{i=1}^{\omega (n)}\alpha _{i}}$.

Például 24 = 2³ × 3¹, így ω(24) = 2 és Ω(24) = 3 + 1 = 4.

• ω(n) értéke n = 1, 2, 3…-ra 0, 1, 1, 1, 1, 2, 1, 1, 1, … (A001221 sorozat az OEIS-ben).
• Ω(n) értéke n = 1, 2, 3…-ra 0, 1, 1, 2, 1, 2, 1, 3, 2, … (A001222 sorozat az OEIS-ben).

Fordítás

• Ez a szócikk részben vagy egészben a Prime factor című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Kapcsolódó szócikkek

• Összetett szám
• Oszthatóság
• Eratoszthenész szitája
• Erdős–Kac-tétel
• Számelméleti függvény

További információk

• Alice és Bob - 16. rész: Alice és Bob alaptétele

Jegyzetek